By Steve Bolton

…………In the last couple of installments of this amateur series of self-tutorials on outlier identification with SQL Server, we dealt with detection methods that required recursive recomputation of the underlying aggregates. This week’s topic, Peirce’s Criterion, also flags outliers in an iterative manner, but doesn’t require the same sliding window to continually recalculate the mean and standard deviation as Chauvenet’s Criterion and the Modified Thomson Tau Test do. Like these analogous methods, Peirce’s Criterion can be made useful to DBAs by using it to merely flag potential outliers and performing new computations as if they had been removed, rather than deleting them without adequate further investigation, as sometimes occurs with the other two. While writing this series, I’ve slowly come to the realization that the statistical formulas underlying many of these methods can be swapped in and out almost like the modularized parts of a car engine, radio kit or DIY computer; for example, Chauvenet’s Criterion and the Modified Thompson Tau test leaven standard hypothesis testing methods with comparisons to Z-Scores, with the former merely substituting thresholds based on a Gaussian normal distribution (i.e. a bell curve) rather than the Student’s T-distribution used in the latter. Peirce’s Criterion is also recursive, but uses the R-values produced by Pearson Product Moment Correlation calculations as thresholds for its Z-Scores. I originally had high hopes for Peirce’s Criterion because those correlation coefficients are easy to calculate on entire databases, but it turns out that lookup tables are required for the R-Values. These are even shorter and more difficult to find on the Internet than the Gaussian and T-distribution lookup tables required for some of the outlier detection methods based on hypothesis testing, which were covered in the last six posts. For that reason, I found it more difficult than usual to validate my T-SQL samples, so be cautious when implementing the code below. Furthermore, the Criterion is burdened with the same requirement for prior goodness-of-fit testing, to prove that the underlying data follows a bell curve.
…………It is not surprising that the Criterion carries so many restrictions, given that it is one of the first outlier detection methods ever devised. The algorithm that mathematician Benjamin Peirce (1809-1880)[1] introduced in an 1852 paper in the Astronomical Journal is indeed difficult to follow and implement, even for those with far more experience than myself. Programmers have apparently had some success recently in coding the underlying math in R and Python[2], but my solution is based on the more accessible version published in 2003 in the Journal of Engineering Technology by Stephen Ross, a professor of mechanical engineering at the University of New Haven.[3] The DDL in Figure 1 can be used to import the table on page 10 to 12, which translates into 540 R-values for up to nine potential outliers and a maximum of 60 records. Denormalizing it into a single interleaved lookup table allows us to access the values in a more legible way with a single join, rather than the double join that would be required with two normalized tables. I altered the algorithm Ross provides to do all of the comparisons in a single iteration, since it is trivial in a set-based language like T-SQL to simply check the nine highest absolute deviations against the corresponding R-Values in one fell swoop. The T3 subquery in Figure 2 simply looks up all nine R-Values for the count of all the records in the dataset, then calculates the MaximumAllowableDeviation values by multiplying them by the standard deviation of the entire dataset. The T2 subquery merely calculates the nine highest absolute deviations in the dataset (using basically the same logic as that found in Z-Scores) and joins them to the NumberOfOutliers of the same rank. If the absolute deviation is higher than the maximum allowable deviation, the record is flagged as an outlier. The rest of the code follows the same format as that of other procedures posted in this series; the first five parameters allow you to select any column in any database for which you have access and @DecimalPrecision enables users to avoid arithmetic overflows. The rest is all dynamic SQL, with the customary debugging comment line above the EXEC. To avoid cluttering the code, I didn’t supply the brackets needed to accommodate spaces in object names – which I don’t allow in my own code – or validation logic, or SQL injection protection. As always, the procedure and lookup table are implemented in a Calculations schema that can be easily changed. Since we can get a bird’s-eye view of all nine rows. as depicted in Figure 3, there’s no reason to incorporate the @OrderByCode parameter used in past tutorials.

Figure 1: DDL for the R-Value Lookup Table
CREATE TABLE [Calculations].[PeirceRValueTable](
       [ID] [smallint] IDENTITY(1,1) NOT NULL,
       [N] [tinyint] NULL,
       [NumberOfOutliers] [tinyint] NOT NULL,
       [RValue] [decimal](4, 3) NULL,
 CONSTRAINT [PK_PeirceRValueTable] PRIMARY KEY CLUSTERED ( [ID] ASC )WITH (PAD_INDEX = OFF, STATISTICS_NORECOMPUTE
= OFF, IGNORE_DUP_KEY = OFF, ALLOW_ROW_LOCKS = ON, ALLOW_PAGE_LOCKS = ON) ON [PRIMARY]) ON [PRIMARY]

Figure 2: Code for the Peirce’s Criterion Stored Procedure
CREATE PROCEDURE [Calculations].[PiercesCriterionSP]
@DatabaseName as nvarchar(128) = NULL, @SchemaName as nvarchar(128), @TableName as nvarchar(128),@ColumnName AS nvarchar(128), @PrimaryKeyName as nvarchar(400), @DecimalPrecision AS nvarchar(50)
AS
DECLARE @SchemaAndTableName nvarchar(400), @SQLString nvarchar(max)
SET @DatabaseName = @DatabaseName + ‘.’
SET @SchemaAndTableName = ISNull(@DatabaseName, ”) + @SchemaName + ‘.’ + @TableName
SET @SQLString = ‘DECLARE @Mean decimal(‘ + @DecimalPrecision + ‘), @StDev decimal(‘ + @DecimalPrecision + ‘), @Count decimal(‘ + @DecimalPrecision + ‘)
SELECT @Count=Count(CAST(‘ + @ColumnName + ‘ AS Decimal(‘ + @DecimalPrecision + ‘))), @Mean = Avg(CAST(‘ + @ColumnName + ‘ AS Decimal(‘ + @DecimalPrecision + ‘))), @StDev = StDev(CAST(‘ + @ColumnName + ‘ AS Decimal(‘ + @DecimalPrecision + ‘)))
FROM ‘ + @SchemaAndTableName + ‘
WHERE ‘ + @ColumnName + ‘ IS NOT NULL

SELECT ‘ + @PrimaryKeyName + ‘, ‘ + @ColumnName + ‘, NumberOfOutliers, AbsoluteDeviation, MaximumAllowableDeviation, ”IsOutlier” = CASE WHEN AbsoluteDeviation > MaximumAllowableDeviation THEN 1 ELSE 0 END
FROM (SELECT TOP 9 ‘ + @PrimaryKeyName + ‘, ‘ + @ColumnName + ‘, AbsoluteDeviation, ROW_NUMBER() OVER (ORDER BY AbsoluteDeviation DESC) AS RN
       FROM (SELECT ‘ + @PrimaryKeyName + ‘, ‘ + @ColumnName + ‘, ABS(‘ + @ColumnName + ‘ – @Mean) AS AbsoluteDeviation
       FROM ‘ + @SchemaAndTableName + ‘
      WHERE ‘ + @ColumnName + ‘ IS NOT NULL) AS T1) AS T2
INNER JOIN   (SELECT NumberOfOutliers, @StDev * RValue AS MaximumAllowableDeviation
      FROM Calculations.PeirceRValueTable
       WHERE N = 60) AS T3@Count
ON RN = NumberOfOutliers‘
–SELECT @SQLString  —uncomment this to debug string errors
EXEC (@SQLString)

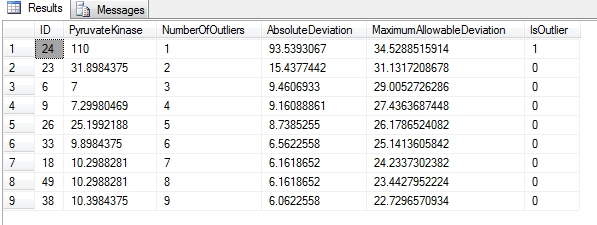
Figure 3: Results for Peirce’s Criterion
EXEC [Calculations].[PiercesCriterionSP]
             @DatabaseName = N’DataMiningProjects‘,
             @SchemaName = N’Health‘,
             @TableName = N’First60RowsPyruvateKinaseView’,
             @ColumnName = N’PyruvateKinase‘,
             @PrimaryKeyName = N’ID’,
              @DecimalPrecision = N’10,7′

…………The results above come from a view on the first 60 rows of a small dataset on the Duchennes form of muscular dystrophy, which I downloaded from the Vanderbilt University’s Department of Biostatistics. I’ve stress-tested some of the procedures I posted earlier in this series on an 11-million-row table of Higgs Boson data made publicly available by the University of California at Irvine’s Machine Learning Repository, but there’s no point in doing that (or posting client statistics and execution plans) with Peirce’s Criterion procedure if we’re limited to 60 rows. In lieu of new algorithms like those used by R and Python to compute the test in far greater detail, this is about as useful as the test can be made in a SQL Server setting. There are some definite advantages over Chauvenet’s Criterion and the Modified Thompson Tau test, in that automatic deletion of records is not encouraged to the same extent and expensive recursive calculations are not necessary. Yet like the last six standard outlier detection methods surveyed here, it’s not really suitable for usage on tables of thousands of rows, let alone the billions used in Big Data applications. As usual, the available lookup tables are simply too small, calculating the missing lookup values is not feasible at this time and the test is only applicable to a Gaussian distribution. One of the pluses is that Peirce’s Criterion does not depend on confidence levels that are typically set by custom rather than sound reasoning. Furthermore, the probabilistic reasoning it is based upon is sound, but does not represent a guarantee; probabilities only generate reasonable expectations but have no effect on outcomes. This drawback of probabilistic stats was recognized long ago by Peirce’s son, but has since been forgotten – especially after the advent of quantum mechanics. As pointed out by Theodore P. Hill and Arno Berger, the authors of a study on Benford’s Law cited earlier in this series, “The eminent logician, mathematician, and philosopher C.S. Peirce once observed [Ga, p.273] that ‘‘in no other branch of mathematics is it so easy for experts to blunder as in probability theory.’’[4] I expected Peirce’s Criterion to be more useful because it is dependent on correlation stats that are common and easy to calculate, but it turns out that it belongs in the same class of outlier detection methods as Grubbs’ Test, the Generalized Extreme Studentized Deviate (GESD) test, Dixon’s Q-Test, the Tietjen-Moore Test, the Modified Thompson Tau test and Chauvenet’s Criterion. The lookup tables may not involve comparisons to Gaussian and T-distribution values like these hypothesis testing methods do, but the drawbacks are largely the same. Work is apparently ongoing in fields that use statistics to make the R-values easier to calculate from ordinary correlation coefficients, so Peirce’s Criterion may wind up being more usable than any of these in the long run. For now, however, SQL Server users would probably be better off sticking with methods like Z-Score and Benford’s Law that are more appropriate to large databases. So far, what I’ve found most striking about my misadventures in this topic to date is just how difficult it is to apply many commonly used statistical tests for outliers to the kind of datasets the SQL Server community works with; I’m only an amateur learning my way in this field, but I wonder at times if our use cases don’t call for the invention of new classes of tests. In the meantime, we can still rely on more useful outlier detection methods like Interquartile Range, which I’ll explain to the best of my inability next week. DBAs are probably also likely to find real uses for the visual detection methods that can be easily implemented in Reporting Services, as well as Cook’s Distance and Mahalanobis Distance, which I’ve saved for the end of the series because the difficulty in coding them appears to be commensurate to their potential value.

[1] The name is not misspelled but is frequently mispronounced as “Pierce” rather than “purse.” The authorship is made even more confusing by the fact that Benjamin’s son, Charles Sanders Peirce (1839-1914), was also a well-known mathematician who published commentaries on his father’s Criterion. Apparently the son fits snugly in the category of mathematicians and physicists with unusual emotional and mental disturbances, given that he was “he was, at first, almost stupefied, and then aloof, cold, depressed, extremely suspicious, impatient of the slightest crossing, and subject to violent outbursts of temper” by trigeminal neuralgia that led to his pattern of “social isolation”; perhaps it also factored into the decision of Harvard’s president to ban him from employment there. He can’t have been entirely irrational though, given that he was very close to William James, one of the few sane American philosophers. For more backstory, see the Wikipedia pages “Benjamin Peirce” and “Charles Sanders Peirce” at http://en.wikipedia.org/wiki/Benjamin_Peirce and http://en.wikipedia.org/wiki/Charles_Sanders_Peirce respectively.

[2] See the Wikipedia page “Peirce’s Criterion,” available at the web address http://en.wikipedia.org/wiki/Peirce%27s_criterion

[3] pp. 3-4, Ross, Stephen M. “Peirce’s Criterion for the Elimination of Suspect Experimental Data,” pp. 1-12 in the Journal of Engineering Technology, Fall 2003. Vol. 2, No. 2. http://newton.newhaven.edu/sross/piercescriterion.pdf

[4] Berger, Arno and Hill , Theodore P., 2011, “Benford’s Law Strikes Back: No Simple Explanation in Sight for Mathematical Gem,” published by Springer Science Business Media, LLC, Vol. 33, No. 1. Available online at http://people.math.gatech.edu/~hill/publications/PAPER%20PDFS/BenfordsLawStrikesBack2011.pdf.