By Steve Bolton

…………In the last three installments of this amateur series of mistutorials on finding outliers using SQL Server, we delved into a subset of standard detection methods taken from the realm of statistical hypothesis testing. These are generally more difficult to apply to tables of thousands of rows, let alone the billions or even trillions commonly associated with the buzzword “Big Data,” for a number of reasons. First, many of them are invalid if the data doesn’t follow a normal distribution, which requires goodness-of-fit testing that can be expensive on large datasets. Secondly, many of them also depend on comparisons to Student’s T and other distributions in order to define a data point as an outlier, but the lookup tables widely available in texts and on the Internet generally stop after sample sizes of a couple of hundred at best. Calculating these for the much larger datasets that DBAs work with is likely to be computationally costly, especially in the case of last week’s topic, the Tietjen-Moore test. Typically, they are used to give a more rigorous numerical definition of an outlier in small dataset of a few dozen or a few hundred data points, which is at least an improvement over simply spotting them by eye in a scatter plot or some other form of data visualization. Hypothesis testing certainly has valid uses when applied to its proper use case, which is proving a single point of evidence, not ferreting out data quality problems or the kind of exploratory data mining DBAs are likely to do. Even then, there are many pitfalls to watch out for, including common misconceptions about probabilistic reasoning and terms like “confidence” and “statistical significance.” The manner in which alpha values are selected to define confidence intervals is also somewhat capricious. I am more confident in hanging my hat on measures like Minimum Description Length and Kolmogorov Complexity which are more deeply rooted in reason, but I’ll have to defer discussion of these for a future series tentatively titled Information Measurement with SQL Server, since they’re not applicable to outlier detection. Despite these caveats, I’ll finish this detour into outlier detection methods dependent on hypothesis testing before getting back on track with topics like Interquartile Range and Cook’s Distance that will probably prove to be more useful to DBAs.
…………For the sake of completeness and finishing what I started, I’ll give a quick rundown of Dixon’s Q-Test, which suffers from many of the limitations listed above. It too is invalid when applied to a dataset that does not follow a Gaussian or “normal” distribution, i.e. a bell curve. The test statistic derived from it must also be compared to a particular distribution, which is much more difficult to find reference lookup tables for than the ubiquitous T-distribution. The DDL in Figure 1 was used hold the critical values I inserted from the only source I could find during a short search, from a webpage at the University of Göttingen’s Department of Sedimentology and Environmental Geology. This particular lookup table only goes up to 25 degrees of freedom, so we can only apply it to datasets with that many rows. Yet the limitations do not end there. As discussed a few columns ago, Grubbs’ Test can only be applied to a single row at a time; Dixon’s Q-Test is even more restrictive, in that it can only be applied to a dataset once, to detect a single outlier. As its Wikipedia entry states, “This assumes normal distribution and per Dean and Dixon, and others, this test should be used sparingly and never more than once in a data set.”[ii] If the 25-record limit wasn’t a fatal blow to its usability, then the single-use criterion certainly delivers the coup de grace. Nevertheless, I’ll provide the stored procedure in Figure 2 for anyone who finds a need for it:

Figure 1: DDL for the Dixon’s Q-Test Critical Value Table
CREATE TABLE [Calculations].[DixonsQTestTable](
[ID] [bigint] IDENTITY(1,1) NOT NULL,
[N] [tinyint] NULL,
[Alpha10] [decimal](4, 3) NULL,
[Alpha05] [decimal](4, 3) NULL,
[Alpha02] [decimal](4, 3) NULL,
[Alpha01] [decimal](4, 3) NULL,
[Alpha005] [decimal](4, 3) NULL,
CONSTRAINT [PK_DixonsQTestTable] PRIMARY KEY CLUSTERED
([ID] ASC)WITH (PAD_INDEX = OFF, STATISTICS_NORECOMPUTE
= OFF, IGNORE_DUP_KEY = OFF, ALLOW_ROW_LOCKS = ON, ALLOW_PAGE_LOCKS = ON) ON [PRIMARY]) ON [PRIMARY]

Figure 2: Code for the Dixon’s Q-Test Procedure
ALTER PROCEDURE [Calculations].[DixonsQTestSP]
@DatabaseName as nvarchar(128) = NULL, @SchemaName as nvarchar(128), @TableName as nvarchar(128),@ColumnName AS nvarchar(128), @PrimaryKeyName as nvarchar(400), @OrderByCode as tinyint = 1, @DecimalPrecision AS nvarchar(50), @Alpha decimal(38,35) = 0.05
AS

SET @DatabaseName = @DatabaseName + ‘.’
DECLARE @SchemaAndTableName nvarchar(400)
SET @SchemaAndTableName = ISNull(@DatabaseName, ”) + @SchemaName + ‘.’ + @TableName

DECLARE @SQLString nvarchar(max)
SET @SQLString = ‘DECLARE @Mean decimal(‘ + @DecimalPrecision + ‘), @Range  decimal(‘ + @DecimalPrecision + ‘), @Count decimal(‘ + @DecimalPrecision + ‘), @CriticalValue decimal(‘ + @DecimalPrecision + ‘), @Alpha
decimal(‘ + @DecimalPrecision + ‘), @OrderByCode tinyint

SET @OrderByCode  = ‘ + CAST(@orderByCode AS nvarchar(50)) + ‘
SET @Alpha = ‘ + CAST(@Alpha AS nvarchar(50)) + ‘

SELECT @Range = Max(CAST(‘ + @ColumnName + ‘ AS decimal(‘ + @DecimalPrecision + ‘))) – Min(CAST(‘ + @ColumnName + ‘ AS decimal(‘ + @DecimalPrecision + ‘))), @Count=Count(CAST(‘ + @ColumnName + ‘ AS Decimal(‘ + @DecimalPrecision + ‘)))
FROM ‘ + @SchemaAndTableName + ‘
WHERE ‘ + @ColumnName + ‘ IS NOT NULL

SELECT @CriticalValue = CASE
      WHEN @Alpha = 0.1 THEN Alpha10
      WHEN @Alpha = 0.05 THEN Alpha05
      WHEN @Alpha = 0.02 THEN Alpha02
      WHEN @Alpha = 0.01 THEN Alpha01
      WHEN @Alpha = 0.005 THEN Alpha005
      ELSE NULL
      END
FROM Calculations.DixonsQTestTable
WHERE N = @Count

SELECT ‘ + @PrimaryKeyName + ‘, ‘ + @ColumnName + ‘, Gap, TestStatistic, @CriticalValue AS Critical’ + @ColumnName + ‘, @Alpha AS Alpha, ”IsOutlier” = CASE WHEN TestStatistic > @CriticalValue THEN 1 WHEN TestStatistic <= @CriticalValue THEN 0 ELSE NULL END
FROM (SELECT ‘ + @PrimaryKeyName + ‘, ‘ + @ColumnName + ‘, Gap, Gap / @Range AS TestStatistic
       FROM  (SELECT ‘ + @PrimaryKeyName + ‘, ‘ + @ColumnName + ‘, Lead(‘ + @ColumnName + ‘, 1, 0) OVER (ORDER BY ‘ + @ColumnName + ‘) – ‘ + @ColumnName + ‘ AS Gap
      FROM ‘ + @SchemaAndTableName + ‘
      WHERE ‘ + @ColumnName + ‘ IS NOT NULL) AS T1) AS T2
ORDER BY CASE WHEN @OrderByCode = 1 THEN ‘ + @PrimaryKeyName + ‘ END ASC,
CASE WHEN @OrderByCode = 2 THEN ‘ + @PrimaryKeyName + ‘ END DESC,
CASE WHEN @OrderByCode = 3 THEN ‘ + @ColumnName + ‘ END ASC,
CASE WHEN @OrderByCode = 4 THEN ‘ + @ColumnName + ‘ END DESC,
CASE WHEN @OrderByCode = 5 THEN TestStatistic END ASC,
CASE WHEN @OrderByCode = 6 THEN TestStatistic END DESC‘

–SELECT @SQLString — uncomment this to debug string errors
EXEC (@SQLString)

…………There’s not much going on here in comparison to some of the more complex procedures I’ve posted recently. The first five parameters allow users to perform the test on any column in any database for which they have requisite permissions. The @DecimalPrecision is a parameter I’ve added to many of my procedures to enable users to escape from arithmetic overflows, while the @OrderByCode takes the same values as in other tutorials: the value 1 orders the results by the primary key ascending, 2 by the same descending, 3 and 4 by the column name ascending or descending respectively, and 5 and 6 order them by the TestStatistic in either direction. Most of the procedure consists of implementations of the @OrderByCode, aggregate retrievals and column selection that I’ve merely cut and pasted from past procedures. The logic of the test statistic itself is quite simple: use the T-SQL Lead windowing function to find the previous row, calculate the gap and then sort by it. The test statistic is merely the gap divided by the range.[iii] Just like with the Tietjen-Moore test in last week’s article, this is probably of greater utility for our use case scenarios than a comparison of a single test statistic to the critical value; for that reason, I’ve returned all 25 rows of a view on the Hemopexin column of the 209 rows of the Duchennes dataset, derived from research on a form of muscular dystrophy that Vanderbilt University’s Department of Biostatistics has made publicly available. These are ordered by the gap and test statistic, which tell us more about the data distribution of the view than a single outlier test would do.

Figure 3: Results for a View on the First 25 Values for the Hemopexin Column
EXEC [Calculations].[DixonsQTestSP] @DatabaseName = N’DataMiningProjects‘, @SchemaName = N’Practice‘, @TableName = N’Top25HemopexinView’, @ColumnName = N’Hemopexin‘, @PrimaryKeyName = N’ID’, @OrderByCode = 6, @DecimalPrecision = N’12,8′, @Alpha = 0.1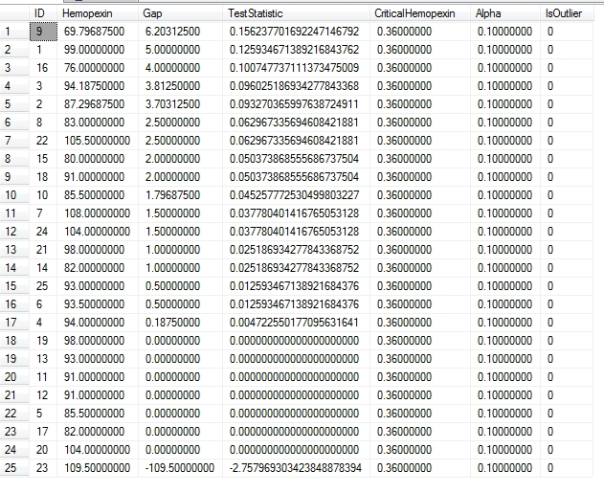

…………There are no outliers in this particular view, according to the comparison made against the critical values cited in the University of Göttingen’s source. It did correctly identify an outlier when I tested it against the example data provided in the Wikipedia entry. The code also works quite quickly, as can be expected for a view of just 25 records; that is why I won’t bother to post execution plans or test it against the much larger Higgs Boson dataset as we have done in previous tutorials to look for performance bottlenecks. It may work as designed, but it is probably more useful when the gaps and test statistics for all of the rows are provided, as depicted in Figure 3. Even when adapted in this way, however, it is of still of little practical utility for datasets with thousands of records, in large part because we don’t have a means of deriving critical values for that many rows. One strategy might be to define a view on a subset of data as I have done above, quite arbitrarily. On the other hand, taking tiny samples of large datasets, even when properly randomized, doesn’t do us much good if our most common purposes are finding and fixing all rows affected by data quality issues, or doing exploratory data mining. When we’re dealing with datasets of billions of records; our main use case is to devise procedures that will ferret out as many of them as we can find, as efficiently as we can – which means getting them all in one pass if possible, not looking for one per test as we do with Grubbs and Dixon. The latter is even more restrictive, because according to the developers of the test itself, it ought not be applied more than once to any dataset. We’re not just limited to testing one outlier in a single pass, but to a single pass, forever. That is obviously not as useful as familiar tests like Z-Scores, which can be applied as often as we like to an entire database. In the next installment of this series we’ll discuss the Modified Thompson Tau test, which is more sophisticated in that it marries Z-Scores to some of the hypothesis testing logic underpinning the last few tutorials. I thought it would turn out to be a shotgun wedding, but it turns out that this test can be enhanced by returning all of the values involved, just as Dixon’s Q-Test can be made mildly more useful in the same way. Such adjustments might be called for in the cases of many of the outlier detection methods based on hypothesis testing, since we’re using them for quite different purposes than what they were designed for. The statistical tools introduced in this segment of the series might not be as useful on an everyday basis to DBAs as upcoming topics like Interquartile Range, Peirce’ Criterion, Cook’s Distance or Mahalanobis Distance, but there’s no reason to remove them from our tool belts if they can be adusted to work with rare use cases that we might eventually encounter.

See the webpage titled “Out?Lier”at the website of the Geowissenschaftliches Zentrum der Universität Göttingen’s Department of Sedimentology and Environmental Geology, which is available at the web address http://www.sediment.uni-goettingen.de/staff/dunkl/software/o_l-help.html

[ii] See the Wikipedia page “Dixon’s Q-Test,” available online at http://en.wikipedia.org/wiki/Dixon%27s_Q_test

[iii] IBID.