By Steve Bolton
…………In the last edition of this amateur series of self-tutorials on goodness-of-fit testing with SQL Server, we discussed the Jarque-Bera Test, a measure that unfortunately doesn’t scale well on datasets of the size that DBAs are accustomed to using. The problem is not with the usefulness of the statistics that it is composed of, because skewness and kurtosis are easy to interpret and valuable in their own right as measures of shape and for purposes of outlier detection. Usually scaling problems signify performance issues, but the resource consumption and execution of the Jarque-Bera Test aren’t bad by any means; the issue is that the statistic itself increases to ungodly numbers that are difficult to interpret, precisely because it was designed with smaller datasets in mind. In this week’s installment, I’ll provide an alternative measure that also builds upon skewness and kurtosis and can be calculated in almost exactly the same amount of time as Jarque-Bera, but without the cumbersome scaling issue.
…………The improved interpretability of D’Agostino’s K-Squared Test comes at the cost of more complicated internal calculations, which turn out to be trivial in comparison to the main computational costs, which consist almost exclusively of index seeks and sorts in the execution plan issued by the SQL Server query optimizer. This added complexity is only a problem if one wants to check to see what’s going on under the hood in these calculations, which is rarely necessary in most use cases after the code has been validated. As I pointed out at every opportunity in my earlier mistutorial series A Rickety Stairway to SQL Server Data Mining, most end users have about as much need to understand how such statistics are derived as the average driver needs to know the engineering details of their car; in many cases it is a mistake to overload them with superfluous information like incomprehensible math equations. That is why I haven’t posted any such formulas in the last few tutorial series I’ve posted here. End users should understand enough to interpret the results in light of their domain knowledge, just as the average rush hour commuter needs to know how to read a gas gauge and transmission fluid stick properly. Those who write the computer code that implement these stats obviously need to grasp the inner workings at a much deeper level, but not to the point that they’re designing their own formulas; data mining programmers essentially occupy the middle zone halfway between end users and mathematicians, in the same way that garage mechanics reside in the niche between drivers and automotive engineers. It is my goal to learn the skills necessary to serve at this midpoint, but as I usually point out, I haven’t reached it yet; I hope to use blog posts of this kind to familiarize myself with these topics better, not because I already know the material well. And that is why I cannot explain in great detail why D’Agostino’s K-Squared Test (a.k.a. the D’Agostino-Pearson Omnibus Test) works as it does. Like a typical mechanic, I was able to get it running sufficiently well that it returns the expected results in a potentially reliable way, but I don’t have sufficient skill to comment on why it was designed as it was. Nevertheless I did pick up a few things while reading sources like D’Agostino, et al.’s 1990 paper in The American Statistician[1] and as usual, the Wikipedia[2] article on the topic, which may not be a professional source but qualifies as the most convenient repository for every math formula under the sun.
…………As you can gather from the T-SQL code in Figure 1, the underlying equations I found in former source are fairly complicated and involve the derivation of several intermediate statistics in between the sample skewness and kurtosis and the final metric. Although the latter source is only an introduction to the topic, it did provide some invaluable insights into the aim of these calculations, albeit without explaining why those particular calculations satisfied those aims. Apparently, the @Z1 and @Z2 measures are meant to bring the skewness and kurtosis in line with the standard normal distribution to solve their “frustratingly slow” approach to the distribution limit, which is a scaling issue of sorts.[3] The SELECT statement towards the end that assigns the final value to the @K2Test combines these internal calculations into a single result so that the skewness and kurtosis can be measured together, in what technically known as an “omnibus test.”[4] After all these esoteric calculations, that final assignment is actually quite simple. I’m sure the nitty gritty details are in the original academic articles published by statisticians Ralph D’Agostino and E.S. Pearson in the early ‘70s, but I couldn’t find any publicly accessible copies; judging from the difficulty I had in following the 1990 paper, much of it would still have been over my head anyways. The important thing to know is that I was able to follow the equations sufficiently well that the code below returns the correct results for the examples provided by D’Agostino, et al.
Figure 1: T-SQL Code for the D’Agostino-Pearson K-Squared Test
CREATE PROCEDURE [Calculations].[NormalityTestDAgostinosKSquaredSP]
@DatabaseName as nvarchar(128) = NULL, @SchemaName as nvarchar(128), @TableName as nvarchar(128),@ColumnName AS nvarchar(128), @PrimaryKeyName as nvarchar(400)
AS
DECLARE @SchemaAndTableName nvarchar(400),@SQLString nvarchar(max)
SET @SchemaAndTableName = @DatabaseName + ‘.’ + @SchemaName + ‘.’ + @TableName
SET @SQLString = ‘DECLARE @Mean float, @StDev float, @Count as bigint, @Alpha decimal(38,37),
@One float = 1, @Two float = 2, @Three float = 3, @Four float = 4, @Five float = 5,
@Six float = 6, @Seven float = 7, @Eight float = 8, @Nine float = 9,
@TwentyFour float = 24, @TwentySeven float = 27, @Seventy float = 70,
@RecpiprocalOfNSampleSize float, @DifferenceFromSampleMeanSquared float, @DifferenceFromSampleMeanCubed
float, @DifferenceFromSampleMeanFourthPower float, @SampleSkewness float, @SampleKurtosis float,
@Y float, @B2 float, @WSquared float, @Z1 float, @Z2 float, @Sigma float, @E float, @VarianceKurtosis float,
@StandardizedKurtosis float, @ThirdStandardizedMomentOfKurtosis float, @A float, @K2Test float
SELECT @Count = Count(‘ + @ColumnName + ‘), @Mean = Avg(CAST(‘ + @ColumnName + ‘ AS float)), @StDev = StDev(‘ + @ColumnName + ‘)
FROM ‘ + @SchemaAndTableName + ‘
WHERE ‘ + @ColumnName + ‘ IS NOT NULL
SELECT @RecpiprocalOfNSampleSize = @One / @Count
DECLARE @CountPlusOne float = @Count + @One, @CountPlusThree float = @Count + @Three, @CountPlusFive float = @Count + @Five,
@CountPlusSeven float = @Count + @Seven, @CountPlusNine float = @Count + @Nine, @CountMinusTwo float = @Count – @Two,
@CountMinusThree float = @Count – @Three
DECLARE @CountPlusOneTimesCountPlusThree float = (@Count + @One) * (@Count + @Three)
SELECT @DifferenceFromSampleMeanSquared = SUM(Power(DifferenceFromSampleMean, 2)) OVER (ORDER BY ‘ + @PrimaryKeyName + ‘ ASC),
@DifferenceFromSampleMeanCubed = SUM(Power(DifferenceFromSampleMean, 3)) OVER (ORDER BY ‘ + @PrimaryKeyName + ‘ ASC),
@DifferenceFromSampleMeanFourthPower =SUM(Power(DifferenceFromSampleMean, 4)) OVER (ORDER BY ‘ + @PrimaryKeyName + ‘ ASC)
FROM (SELECT ‘ + @PrimaryKeyName + ‘, CAST(‘ + @ColumnName + ‘ AS float) – @Mean as DifferenceFromSampleMean — make a single pass across the table?
FROM ‘ + @SchemaAndTableName + ‘
WHERE ‘ + @ColumnName + ‘ IS NOT NULL) AS T1
SELECT @SampleSkewness = (@RecpiprocalOfNSampleSize * @DifferenceFromSampleMeanCubed) /(Power((@RecpiprocalOfNSampleSize * @DifferenceFromSampleMeanSquared), 1.5))
SELECT @SampleKurtosis = (@RecpiprocalOfNSampleSize * @DifferenceFromSampleMeanFourthPower) /(Power((@RecpiprocalOfNSampleSize * @DifferenceFromSampleMeanSquared), 2))
— perform operations on the Skewness
SELECT @Y = @SampleSkewness * Power(((@CountPlusOneTimesCountPlusThree) / (@CountMinusTwo * @Six)), 0.5) — do the brackets signify multiplication? ****
SELECT @B2 = (@CountPlusOneTimesCountPlusThree * (@Three * ((Power(@Count, 2) + (@TwentySeven * @Count)) -@Seventy))) / (@CountMinusTwo * @CountPlusFive * (@Count + @Seven) * (@Count + @Nine))
SELECT @WSquared = Power(@Two * (@B2 – @One), 0.5) – @One
SELECT @Alpha = Power(Abs(@Two / (@WSquared – @One)), 0.5)
SELECT @Sigma = @One / (Power(Abs((Log(Abs(Power(@WSquared, 0.5))))), 0.5))
— Im not sure if this sigma is related to StDev or not
SELECT @Z1 = @Sigma * Log((@Y / @Alpha) + Power((Power((@Y / @Alpha), 2) + @One), 0.5))
SET @SQLString = @SQLString + ‘— perform operations on the kurtosis
SELECT @E = (@Three * (@Count – @One)) / @CountPlusOne — according to the paper, this is the mean for the kurtosis
SELECT @VarianceKurtosis = (@TwentyFour * @Count * @CountMinusTwo * @CountMinusThree) / (Power(@CountPlusOne, 2) * @CountPlusThree * @CountPlusFive
SELECT @StandardizedKurtosis = (@SampleKurtosis – @E) / Power(@VarianceKurtosis, 0.5)
SELECT @ThirdStandardizedMomentOfKurtosis = ((@Six * ((Power(@Count, 2) – (@Five * @Count)) + @Two)) / (@CountPlusSeven * @CountPlusNine)) *
Power((@Six * @CountPlusThree * @CountPlusFive) / (@Count * @CountMinusTwo * @CountMinusThree), 0.5)
SELECT @A = @Six + ((@Eight / @ThirdStandardizedMomentOfKurtosis) * ((@Two / @ThirdStandardizedMomentOfKurtosis) + Power(@One + (@Four / @ThirdStandardizedMomentOfKurtosis), 0.5)))
SELECT @Z2 = ((@One – (@Two / (@Nine * @A))) – Power((@One – (@Two / @A)) / (@One + (@StandardizedKurtosis * Power((@Two / (@A – @Four)), 0.5))), (@One / @Three))) / Power((@Two / (@Nine *
@A)), 0.5)
SELECT @K2Test = Power(@Z1, 2) + Power(@Z2, 2)
— uncomment this to debug the internal calculations SELECT @Alpha, @Sigma, @Y AS T, @B2 AS B2, @WSquared AS WSquared, @E AS E, @VarianceKurtosis AS VarianceKurtosis, @StandardizedKurtosis AS StandardizedKurtosis, @ThirdStandardizedMomentOfKurtosis
AS ThirdStandardizedmMomentOfKurtosis, @A AS A, @DifferenceFromSampleMeanSquared, @RecpiprocalOfNSampleSize, @DifferenceFromSampleMeanSquared, @DifferenceFromSampleMeanCubed, @DifferenceFromSampleMeanFourthPower
SELECT @K2Test AS KSquaredTest, @SampleSkewness AS SampleSkewness, @SampleKurtosis AS SampleKurtosis, @Z1 as Z1, @Z2 as Z2, @Mean AS Mean, @StDev AS StDev‘
–SELECT @SQLString — uncomment this
to debug dynamic SQL errors
EXEC (@SQLString)
…………A few explanations of why the code was written as it was are in order. The five parameters allow users to run the test on any table or view in any database they have sufficient access to, while the first declaration assists in implementing this. The dynamic SQL differs from some of the procedures I’ve posted in the past by the sheer number of reciprocals and constants that need to be precalculated early on, in order to avoid performing the same operations over again. The length of the dynamic SQL also necessitates the use of the second SET statement on the @SQLString, since such strings can’t be assigned in one big gulp after a certain character limit, but can thankfully be added together easily; keep in mind that if this step is left out, the dynamic SQL may be unexpectedly truncated. This procedure also differs in the sense that I’ve chosen to use floats rather than the decimal data type, for the same reason I did in the article on Jarque-Bera: some of the internal calculations are performed on very small fractions, particularly the exponents and reciprocals, which SQL Server will sometimes convert to zeros in the case of the decimal data type. Secondly, I substituted named variables for many of the constants, such as @CountPlusOne, which are declared near the beginning of the dynamic SQL. This is due to the fact that SQL Server sometimes truncates the decimal points out of certain operations on integers; I haven’t yet determined precisely what causes this, although using integers as dividends seems to trigger it most often. Consider this an experiment in discerning whether using named variables is more legible than using countless CAST operations, some of which would have to be buried deep within subqueries. By all means, feel free to copy and paste the constants back in if you know the answers to those questions. As with the Jarque-Bera Test, I’m not certain whether this K2 Test would retain its validity if we substituted the simpler calculations for the full population for the sample skewness and sample kurtosis, but those stats would be preferable if this was case. As usual, I’ve provided a couple of lines of debugging code that can be uncommented if you need to adjust or verify the code, both near the end of the procedure. Be aware that due my difficulty in reading the original equations, @StandardizedKurtosis may need to serve as the root instead of 0.5 (the square root) in my calculation for @Z2, and also in the calculation for the third standardized moment – but I doubt it, since this would throw off the calculations quite a bit. I also added several ABS function calls to avoid Invalid Floating Point Operation errors on T-SQL functions like POWER that can’t handle imaginary roots, but this departure doesn’t seem to affect the final results.
…………The bottom line is that I tested this against the same stem-and-leaf plot cholesterol data from the Framingham Heart Study that D’Agostino, et al. assessed their equations with and get pretty much the same results.[5] They got 1.02 and 4.58 for their sample skewness and kurtosis and 14.75 for the final K2 test statistic, which was derived from Z1 and Z2 values of 3.14 and 2.21 respectively; my results were 1.0235482596477, 4.57738778764656 and 14.7958406166879 for the sample skewness, kurtosis and test statistic respectively, which were derived from values of 3.13939241925962 and 2.22262364213628 for the intermediate Z1 and Z2 stats. It is possible that the slight differences are due to undiscovered errors in my code, but some departure is expected given that I used variables and constants of much higher precision, which would lead to rounding discrepancies. I then tested it against two datasets I’ve been using throughout the last two tutorial series, one on the Duchennes form of muscular dystrophy made publicly available by the Vanderbilt University’s Department of Biostatistics and another on the Higgs Boson that can be downloaded from the University of California at Irvine’s Machine Learning Repository. I derived the first resultset in Figure 2 from the query above it and the following two from queries like it on the first two float columns in the Higgs Boson dataset. Note that test statistic is much larger for the Higgs Boson results – mainly because that table has 11 million rows, compared to just 209 for the Duchennes table – but isn’t quite as inflated as in some of the Jarque-Bera results. One of them has seven digits to the left of the decimal point, which I’d wager is near the limit of numerical legibility for most people. Once you get past that, most people have trouble comparing numbers by eye without resorting to the ungainly strategy of counting digits and mentally interpolating commas between every set of three.
Figure 2: Sample Results from the Duchennes and Higgs Boson Datasets
EXEC [Calculations].[NormalityTestDAgostinosKSquaredSP]
@DatabaseName = N’DataMiningProjects’,
@SchemaName = N’Health’,
@TableName = N’DuchennesTable’
@ColumnName = N’LactateDehydrogenase’,
@PrimaryKeyName = N’ID’

…………The good news is that the procedure performed unexpectedly well; in fact, the first trial run took 3:43 on the first float column in the Higgs Boson table, i.e. exactly the same execution time as for the Jarque-Bera Test in the last tutorial. After all of those arcane calculations you’d expect to see a rather messy execution plan, but as Figure 3 shows, this procedure isn’t all that hard to follow. The main costs were incurred by two non-clustered index seeks and a sort. This is because almost all of the work occurs in retrieving the values and performing simple calculations for each row, not in the fancy math that occurs after they’ve been summarized, which turns out to have an inconsequential computation cost. The main burden of these calculations falls exactly where we want it: on the brains of the coders and testers, not on the end users, to whom the procedure will be a well-oiled black box after error-checking, validation and SQL injection protection code are added.
Figure 3: Execution Plan for the D’Agostino-Pearson Omnibus Test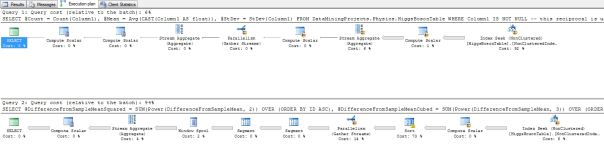
…………There’s more good news: since most of the performance cost occurs in the same seeks, sorts and initial calculations of skewness and kurtosis that the Jarque-Bera Test uses, there’s no real penalty incurred by computing it together with the D’Agostino-Pearson Omnibus Test. If we had to sacrifice one, however, it would be the former, since I have heard anecdotes about statisticians preferring the latter, but not the other way around. One of the reasons the K2 is favored is because of numerous studies (including some written by D’Agostino Sr.) demonstrating that it has better statistical power, which is a numerical measure of how often the actual effects of a variable are detected by a particular test.[6] This metric is applicable to large sample sizes, unlike the Shapiro-Wilk Test[7], and can be used for both one-sided and two-sided hypothesis tests.[8] As I learn more about the field I’m shying more and more away from hypothesis tests, on the grounds that the small sample sizes and narrow focus aren’t suited to typical SQL Server user scenarios, like exploratory data mining on large datasets. Nevertheless, it doesn’t hurt to know that the D’Agostino-Pearson Test is flexible enough to be used for these purposes. Moreover, it can apparently be applied to goodness-of-fit testing on datasets that don’t follow the Gaussian or “normal” distribution, i.e. the bell curve, which isn’t true of many of them. In fact, the authors of that 1990 study go so far as to say that “The extensive power studies just mentioned have also demonstrated convincingly that the old warhorses, the chi-squared test and the Kolmogorov test (1933), have poor power properties and should not be used when testing for normality.”[9] This is by no means the first time I’ve heard such sentiments expressed by statisticians about these two rival metrics, which still seem to be implemented far more frequently in practice despite such advice.
…………Later on in this series I’ll explain how to implement both the Chi-Squared Test and Kolmogorov-Smirnov Test in T-SQL, but I’m going to skip over a couple of other measures related to skewness and kurtosis, at least for the time being. One of these is Mardia’s multivariate versions of skewness and kurtosis, which I will save for some far-flung future when grappling with the complexity added by dealing with multiple columns isn’t too overwhelming; perhaps someday I’ll tack a segment onto the end of this series for multivariate goodness-of-fit tests, like the Cox-Small Test and Smith and Jain’s Test.[10] I’ve organized this series in the order of how difficult the concepts and underlying code are, which brings us to the topic of regression-related methods of goodness-of-fit testing. As explained in the last article, skewness and kurtosis really aren’t that hard to grasp intuitively, and as I dealt with in A Rickety Stairway to SQL Server Data Mining, Algorithm 2: Linear Regression, the core concepts behind regression aren’t that difficult either. The variants of regression can get quite complicated, but drawing a line on a graph based on the relationship between two variables is something every college freshman has been exposed to. The stats based on these lines can also vary in their intricacy; there is apparently even a version of Jarque-Bera for multiple regression[11], which I’ll skip over for now to avoid the added complexity of dealing with three or more variables. The code required to implement regression stats for purposes of normality testing can also require differing levels of sophistication, as we’ll see shortly after New Year’s.
[1] D’Agostino, Ralph B.; Belanger, Albert and D’Agostino Jr., Ralph B, 1990, “A Suggestion for Using Powerful and Informative Tests of Normality,” pp. 316–321 in The American Statistician. Vol. 44, No. 4. Available online at http://www.ohio.edu/plantbio/staff/mccarthy/quantmet/D’Agostino.pdf
[2] See the Wikipedia article “D’Agostino’s K-Squared Test” at http://en.wikipedia.org/wiki/D’Agostino’s_K-squared_test
[3] IBID.
[4] “D’Agostino and Pearson (1973) presented a statistic that combines….to produce an omnibus test of normality. By omnibus, we mean it is able to detect deviations from normality due to either skewness or kurtosis.” See p. 318, D’Agostino, et al., 1990.
[5] IBID., p. 318.
[6] For a better explanation of the term than I can give, see Hopkins, Will G., 2001, “Generalizing to a Population: ESTIMATING SAMPLE SIZE continued,” published at the A New View of Statistics web address http://www.sportsci.org/resource/stats/ssdetermine.html. I highly recommend his website for those who are new to the field of stats, like me.
[7] p. 319, D’Agostino, et al., 1990.
[8] IBID., p. 318.
[9] IBID., p. 316.
[10] I don’t know anything about these tests, but I’ve seen them mentioned in sources like the Wikipedia article “Multivariate Normal Distribution” at http://en.wikipedia.org/wiki/Multivariate_normal_distribution
[11] See the Wikipedia page “Jarque-Bera Test” at http://en.wikipedia.org/wiki/Jarque%E2%80%93Bera_test



