"Dad, can you help me with my homework"? The phrase every parent dreads, particularly as you know it's maths night. The eldest is fiddling with his iPad doing something complicated while Grandpa looks on muttering that in his day silicon based tablets were smaller and came with proper chalk!
A quick peak reveals that the offspring has been asked to write about Pascal's triangle and its usage. The triangle itself has a number of interesting properties and is extremely useful for demonstrating probability.
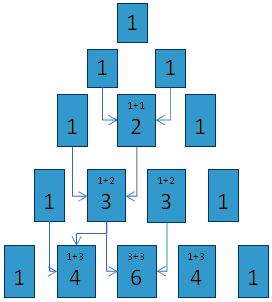
So what has Pascal's triangle got to do with root cause analysis?
Pascal's triangle and the number of components in a system
Let us start by laying out the triangle slightly differently.
| No of components in system | Ways of the system working | Number of components failing | Total | ||||
|---|---|---|---|---|---|---|---|
| 1 component | 2 component | 3 component failures | 4 component failures | All failing | |||
| 1 | 1 | 1 | 1 | 2 | |||
| 2 | 1 | 2 | 1 | 3 | 4 | ||
| 3 | 1 | 3 | 3 | 1 | 7 | 8 | |
| 4 | 1 | 4 | 6 | 4 | 1 | 15 | 16 |
In this case Pascal's triangle can actually tell us the number of ways a system can break. So if we look at a 4 component with components A, B, C, D in the system it works out as follows
| Components failing | Combinations | Examples |
|---|---|---|
| 0 | 1 | A, B, C & D all functioning |
| 1 | 4 | A or B or C or D |
| 2 | 6 | A & B A & C A & D B & C B & D C & D |
| 3 | 4 | A & B & C A & B & D A & C & D B & C & D |
| 4 | 1 | A, B, C & D |
When you consider the number of components that make up a fairly average family car it is a wonder it even moves, let alone surviving the rigours of family life for 100,000+ miles!
Handy maths for working out Pascal's triangle
Any row in Pascal's triangle can be worked out from the one above but if you don't fancy calculating hundreds or thousands of rows there are mathematical formulae to help work it out.
First, there are three mathematical terms you are going to need to know
| Term | Symbol | Example | Description |
|---|---|---|---|
| Factorial | ! | 6! | 1x2x3x4x5x6 = 720 The Excel function for this is FACT |
| Combination | nCr | 6C2 | There are a number of ways of choosing 2 values from 6 when we don't care what order of the chosen values. The Excel function for this is COMBIN This function is how we calculate a row for the triangle n! r!(n-r)! Take the example of the UK National Lottery where the jackpot selection requires you to choose 6 numbers from 49 49! 6!x43! So you have 13,983,816 combinations. In other words, if you are hoping for a lottery jackpot to win you a comfy retirement you'd better have a backup plan. |
| Permutation | nPr | 6P2 | The number of ways of choosing 2 values from 6 if we want them in a specific order. The Excel function for this is PERMUT n! (n-r)! |
T-SQL Functions to calculate factorials, permutations and combinations
As these functions are likely to be used by people with a knowledge of the Excel equivalents I am going to build my T-SQL functions using the same names.
- FACT
- PERMUT
- COMBIN
As I always build my scripts to be repeatable I start with a simple bit of T-SQL to drop my functions. This is exactly the same technique I use when building rollback scripts.
DECLARE @SQL varchar(max), @CRLF CHAR(2)
SET @CRLF = CHAR(13)+CHAR(10)
SELECT @SQL = COALESCE(@SQL + ';'+ @CRLF,'')
+'DROP FUNCTION dbo.'
+ROUTINE_NAME
FROM INFORMATION_SCHEMA.ROUTINES
WHERE ROUTINE_TYPE='FUNCTION'
AND ROUTINE_NAME IN (
'COMBIN',
'PERMUT',
'FACT'
)
PRINT @SQL
EXEC(@SQL)
GOT-SQL Factorial function
Short of using CLR functions I've found that Frank Kalis' method of calculating factorials is the most effective up to 170! in T-SQL
CREATE FUNCTION dbo.FACT(@Factorial AS TINYINT) RETURNS FLOAT
AS
BEGIN
DECLARE @a FLOAT
SET @a = 1
SELECT @a = @a * Number
FROM master..spt_values
WHERE Number BETWEEN 1 AND @Factorial
AND Type='P'
RETURN @a
END
GO
IF @@ERROR = 0
PRINT 'FUNCTION CREATED: dbo.FACT'
GO
If we use this function on values greater than 170 we will get a mathematical overflow error message
Msg 8115, Level 16, State 2, Line 11
Arithmetic overflow error converting expression to data type float.If we SET STATISTICS IO ON and run the body of the function outside of the function (we do this because running statements inside functions mask statistics) we would see a message similar to the following
Table 'spt_values'. Scan count 1, logical reads 4, physical reads 0, read-ahead
reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0.It may be that a factorial function is one that we don't use very often and 4 reads is something we don't worry about but consider the following
- We already know that the function will not work for values over 170
- Exception handling is expensive in any language.
An alternative approach would be to check to see if the argument exceeds 170 and simply not execute the body of the function. If that approach was taken then the following would be true: -
- There would be no reads against the master..stp_values
- There would be no exception generated
- The value returned would be NULL so whatever called the function would have to cater for such a value. This may or may not be a big deal for you.
Our modified function would be as follows
CREATE FUNCTION dbo.FACT(@Factorial AS TINYINT) RETURNS FLOAT
AS
BEGIN
DECLARE @a FLOAT
IF @Factorial<=170
BEGIN
SET @a = 1
SELECT @a = @a * Number
FROM master..spt_values
WHERE Number BETWEEN 1 AND @Factorial
AND Type='P'
END
RETURN @a
END
GO
IF @@ERROR = 0
PRINT 'FUNCTION CREATED: dbo.FACT'
GO
T-SQL Permutation function
Although our factorial function can only handle numbers up to 170 and permutations and combinations depend on factorial functions it is actually possible for a permutation function to cater for higher values.
This is due to basic algebra. Take the example where n=7 and r = 3
| n! (n-r)! | 7! (7-3)! | = | 7! 4! | = | = | 5x6x7 = 210 |
Our lower figure cancels out part of our lower figure hence we can deal with much higher values.
CREATE FUNCTION dbo.PERMUT(@n INT, @r INT) RETURNS FLOAT
AS
BEGIN
DECLARE @a FLOAT
SET @a = 1
SELECT @a = @a * Number
FROM master..spt_values
WHERE Number BETWEEN 1+(@n-@r) AND @n
AND Type='P'
RETURN @a
END
GO
IF @@ERROR = 0
PRINT 'FUNCTION CREATED: dbo.PERMUT'
GO
T-SQL Combination function
When we deal with combinations we don't care about the order in which our selected values appear so there will be far fewer combinations than there are permutations.
In fact our Combination function can actually utilise our Permutation and Factorial functions
CREATE FUNCTION dbo.COMBIN(@n INT, @r INT) RETURNS FLOAT
AS
BEGIN
RETURN dbo.PERMUT(@n,@r) / dbo.FACT(@r)
END
GO
IF @@ERROR = 0
PRINT 'FUNCTION CREATED: dbo.COMBIN'
GO
This is fine up to a point but because our Factorial function can only handle values up to 170 our combination function would also be limited to selecting values from a maximum of 170. In short our combination function couldn't be used to work out ways of selecting 171 values from 172 even though the answer is 172.
If we want to maximize the range of values our combination function deals with what we have to do is look at the bottom half of the nCr equation which is r!(n-r)! and for our arguments we need to work out whether r! or (n-r)! is greater. In other words is the number of values we want to select greater than half the total number of numbers?
Whichever term is greater is the one we want to feed into our Permut function because this will cancel out the most from our factorial equation.
ALTER FUNCTION dbo.COMBIN(@n INT, @r INT) RETURNS FLOAT
AS
BEGIN
DECLARE @Result FLOAT
IF @r > (@n/2)
SET @Result= dbo.PERMUT(@n,(@n - @r)) / dbo.FACT((@n - @r))
ELSE
SET @Result= dbo.PERMUT(@n,@R) / dbo.FACT(@r)
RETURN @Result
END
GO
Back to root cause analysis
Using our new functions we can see that if our system has 64 components then we have 1 way for it to work and 18,446,744,073,709,551,615 ways to screw up.
Of course you would have to be cursed by the Gods to have such a number of failures and the chances are that a system failure would manifest itself in a way that at least gives you an indicator where the problem lies so Pascal's triangle is a farcical model for system failures. A farce being defined as follows.
A highly improbable situation, exaggerated scenarios, and tangental subjects used to illustrate a point.
There are however cases where it should serve as a timely warning for architects and developers.
- When good software development principles are ignored
- When new technologies are introduced within projects
Ignoring Software Principles
Two of the most important principles in software development are that software components should be strongly cohesive and loosely coupled.
Strongly cohesive components are those within a software system that fulfill a clear and unique responsibility and the functions within any component are directly relevant to the operation of that component and only that component.
Let us suppose that you have a customer processing component and an inventory management component. If you build these components where the functional responsibilities of these components are blurred or shared then, in the event of your system breaking, it won't be obvious which component has actually broken!
Loose coupling of components within a system is where a failure in one should not break the entire system due to dependencies on other and/or unrelated components.
If you ignore these principles then you will find that a problem that manifests itself as a problem with customer processing could in actual fact have its origins in the inventory management component.
To put it mildly you will have a system that is difficult to debug and a nightmare to maintain. If you start to audit such a system you will notice the following: -
- The ballooning of the number of possible failure routes described above
- The complex interactions and hand over of responsibilities between components becomes hard to track.
If you have such a system then the chances are you probably have a "hero" culture where a few select individuals know precisely how a system works, probably because they had a hand in writing it!
The implications of new technologies
A business adopts new technology because it harbours a belief that it will bestow in it a competitive advantage or at least keep it abreast of its competitors.
Individuals adopt new technology for a number of reasons
- Technology 'X' is interesting and our jobs would be deathly dull without the thrill of the new
- We want to remain current in the job market and technology 'X' would look good on our CV
- Technology 'X' has the potential to eliminate or at least reduce the work involved in a mundane task.
Technology 'X' itself isn't a problem and neither is Technology Y, Z, Alpha and Omega but when implementing them all together the number of potential failure points illustrated by Pascal's triangle should raise a note of caution.
Technology X, Y, Z, Alpha and Omega may be fault free and brilliant but when new technologies are implemented their newness and a lack of clear understanding as to their strengths and weaknesses can result in faults that are errors in implementation rather than true errors.
- Learning a new technology is fun and exciting
- Learning two new technologies is fun and challenging
- Learning a plethora of technologies and having to deliver to a tight deadline is not fun and extremely stressful.
To contribute another thought to the adoptions of new technology, if you use Pascal's triangle as an indicator then the complexity of the technology may be such that you upweight what the model tells you. Instead of saying technology X, Y & Z represent a component each you may decide that technology Y is complex enough to merit a score of 2 so instead of 3 components you assess the risk as if you have 4 components.
More gloom from a professional pessimist
How many times have you dealt with a problem where the cause turned out to be something totally different and seemingly unrelated to what you expected?
If you have the complex interactions between components all of a sudden it starts to matter whether it is A followed by B rather than B followed by A and this has a dramatic affect on the number of possibilities for failure.
Using the UK National Lottery example if we had to pick the 6 numbered balls in the correct order we would go from 1 chance in 13 million to 1 change in over 10 billion!
Concluding thoughts
You should take my use of Pascal's triangle with a pinch of salt. As I said it is a farce/parody illustrating a point. It has not proven that: -
- Your project is mathematically proven to be doomed to failure
- You will never win the lottery although it is an improbably occurrence
The FACT, PERMUT and COMBIN functions shown in the article are used extensively in probability modelling. FACT in particular crops up in all sorts of formulae used to model customer/prospect behaviour.
If you are interested in data itself rather than just the mechanics of looking after data then there are a wealth of stats functions that data analysts would give there eye teeth to have available to them in the database. If you enjoy programming, whether T-SQL or CLR functions then stats functions represent an interesting challenge.






