Introduction
This article shows how common table expressions (CTE) in SQL Server are naturally suited for navigating trees, such as finding its longest path, or diameter.
Recall that a tree is an undirected graph where unique paths exist between any two nodes (i.e. vertices). Any node may be selected as its top node, with its own collection of paths from it to its leaves. A popular algorithm for finding the longest path in any tree is the following:
- Choose any node as its top node
- Find the longest path from it to its leaves
- Change the top node to the leaf of that path
- Then find the longest path from that leaf to its own leaves
- That path will have maximum length among all paths in the tree
This recipe is very efficient since only two breadth-first searches are required.
For example, consider the following tree:
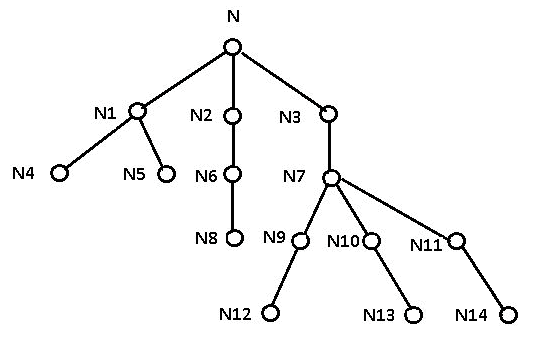
Choose N as the top node and find the longest path from it to its leaves:

Now change the top node of the tree to the leaf of that longest path (N13) and find the longest path from it to one of its own leaves (N8):
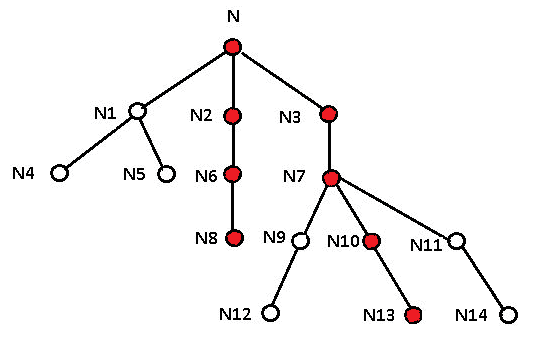
Then that path N13 --> N10 --> N7 --> N3 --> N --> N2 --> N6 --> N8 is the longest path in the tree.
The next section provides a simple script to find the longest path in any tree. After that, a proof that the algorithm always works will be presented, using high school algebra.
Script
The following script builds the above tree and finds the longest path in it. By removing the tree-building snippet, you may refer it to any other tree (replace [Tree] with [My Tree] for example). But note that the script will always change the top node, so if you run it again, you may get a different longest path. In any event, you may wish to add a section that changes it back.
-------------
-- Build tree
-------------
IF EXISTS (SELECT * FROM sys.objects WHERE object_id = OBJECT_ID(N'[dbo].[Tree]') AND type in (N'U'))
BEGIN
TRUNCATE TABLE [dbo].[Tree]
DROP TABLE [dbo].[Tree]
END
CREATE TABLE dbo.[Tree](
NodeId INT IDENTITY(0,1) PRIMARY KEY,
Node VARCHAR(128) NOT NULL,
ParentId INT NULL,
FOREIGN KEY (ParentId) REFERENCES dbo.[Tree](NodeId)
)
-----------------------------------------------------------
-- Populate tree
--
-- Note that insertions must respect referential integrity.
-- So foreign keys must point to records already inserted.
-----------------------------------------------------------
SET NOCOUNT ON
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N',NULL)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N1',0)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N2',0)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N3',0)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N4',1)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N5',1)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N6',2)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N7',3)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N8',6)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N9',7)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N10',7)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N11',7)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N12',9)
INSERT INTO dbo.[Tree](Node,ParentId) VALUES('N13',10)
------------------------------------
-- Find a longest path from top node
-- Get the NodeId of the leaf node
-- This will be the new top node
------------------------------------
DECLARE @NodeIdLeafINT
IF OBJECT_ID(N'tempdb..#r') IS NOT NULL
DROP TABLE #r;
WITH cte (NodeId, Node, ParentId, Level, Path) AS (
SELECT NodeId, Node, ParentId, 0 AS Level,
CAST(Node AS VARCHAR(MAX)) AS Path
FROM dbo.[Tree]
WHERE NodeId = (SELECT TOP 1 NodeId FROM dbo.[Tree] WHERE ParentId IS NULL)
UNION ALL
SELECT T.NodeId, T.Node, T.ParentId, cte.Level + 1 AS Level,
CAST(cte.Path + ' ---> ' + T.Node AS VARCHAR(MAX)) AS Path
FROM dbo.[Tree] T
INNER JOIN cte ON cte.NodeId = T.ParentId
)
SELECT NodeId, Level, Path INTO #r
FROM cte
ORDER BY Path ASC
SELECT TOP 1 @NodeIdLeaf = NodeId FROM #r ORDER BY Level Desc
--------------------------------------
-- Make the leaf node the new top node
--------------------------------------
SET NOCOUNT ON
IF OBJECT_ID(N'tempdb..#s') IS NOT NULL
DROP TABLE #s;
IF OBJECT_ID(N'tempdb..#e') IS NOT NULL
DROP TABLE #e;
WITH cte2 (NodeId, Node, ParentId, Level, Path) AS (
SELECT NodeId, Node, ParentId, 0 AS Level,
CAST(Node AS VARCHAR(MAX)) AS Path
FROM dbo.[Tree]
WHERE NodeId = @NodeIdLeaf
UNION ALL
SELECT T.NodeId, T.Node, T.ParentId, cte2.Level + 1 AS Level,
CAST(cte2.Path + ' ---> ' + T.Node AS VARCHAR(MAX)) AS Path
FROM dbo.[Tree] T
INNER JOIN cte2 ON cte2.ParentId = T.NodeId
)
SELECT NodeId, ParentId INTO #s
FROM cte2
WHERE ParentId IS NOT NULL
SELECT '
UPDATE dbo.[Tree] SET ParentId = NULL WHERE NodeId IN (' +
CAST(NodeId AS VARCHAR(16)) + ',' +
CAST(ParentId AS VARCHAR(16)) + ')' AS SQL,
1 AS Priority
INTO #e FROM #s
INSERT INTO #e(SQL,Priority)
SELECT 'UPDATE dbo.[Tree] SET ParentId = ' + CAST(NodeId AS VARCHAR(16)) +
' WHERE NodeId = ' + CAST(ParentId AS VARCHAR(16)), 2 FROM #s
DECLARE @SQL NVARCHAR(MAX)
-- Declare cursor for #e
-- Date-stamp its name to keep it apart from future scripts or procs
DECLARE curTable20210201 CURSOR
FOR
SELECT SQL FROM #e ORDER BY Priority
FOR READ ONLY
-- Open cursor
OPEN curTable20210201
-- Fetch first row
FETCH NEXT FROM curTable20210201 INTO @SQL
-- Do this for each fetched row
While @@FETCH_STATUS = 0
BEGIN
-- Execute SQL
EXEC sp_executesql @SQL
-- Fetch next row
FETCH NEXT FROM curTable20210201 INTO @SQL
END
-- Close cursor
CLOSE curTable20210201
-- Deallocate cursor
DEALLOCATE curTable20210201
--------------------------------------------
-- Find a longest path from the new top node
-- This is the longest path in the tree
--------------------------------------------
IF OBJECT_ID(N'tempdb..#t') IS NOT NULL
DROP TABLE #t;
WITH cte (NodeId, Node, ParentId, Level, Path) AS (
SELECT NodeId, Node, ParentId, 0 AS Level,
CAST(Node AS VARCHAR(MAX)) AS Path
FROM dbo.[Tree]
WHERE NodeId = @NodeIdLeaf
UNION ALL
SELECT T.NodeId, T.Node, T.ParentId, cte.Level + 1 AS Level,
CAST(cte.Path + ' ---> ' + T.Node AS VARCHAR(MAX)) AS Path
FROM dbo.[Tree] T
INNER JOIN cte ON cte.NodeId = T.ParentId
)
SELECT NodeId, Level, Path INTO #t
FROM cte
ORDER BY Path ASC
SELECT TOP 1 Path FROM #t ORDER BY Level DescHow The Script Works
The first CTE finds the longest path from the top node to one of its leaves, capturing that leaf’s database key for the next operation. The common table expression defines and populates a virtual table cte(NodeId, Node, ParentId, Level, Path) whose rows contain the following information:
NodeId Key Node Node name ParentId Foreign key to parent node Level Number of steps from top node Path Path from top node to this node
Each row represents a node in the tree, along with information about where it sits in that tree. The first SELECT statement selects the top node (i.e. where ParentId is NULL) whose path is simply the node name. The second SELECT statement joins cte with the tree to obtain those nodes X who are children of the top node N, and computes its paths as N --> X.
Since that SELECT statement includes a reference to the CTE that’s being built, it will be executed repeatedly, so the children of the children will be obtained, and so on. Each time, the path to those descendants will be computed by simply adding the new nodes to the existing paths of their parents.
This process repeats until no more additions to the CTE can be obtained. After that, a SELECT statement copies cte to a temporary table, allowing another SELECT statement to select one of the nodes (i.e. records) with the highest level, and corresponding path, which will be the longest path from the top node to its leaves. Then the script uses a CTE to walk along that path, generating UPDATE statements for execution by a subsequent cursor in order to reverse the ParentId of each node on that path. This will make the leaf node the new top level node.
Finally, the original CTE is repeated, but starting at the new top node. This will build the longest path to its own leaves. That path will also be the longest path in the tree.
Proof
Presented here is a detailed explanation of David Eisenstat’s elegant proof that the algorithm always works [1]. His algebraic reasoning (shown in boxes) is untouched from the original, but detailed annotations outside the boxes provide additional clarity.
/*
A maximum path from node s to node t is selected. A node u is arbitrarily selected as the top node of the tree. The goal is to show that any node with maximum distance from this top node will always be the end point of some maximum path. This would prove that the algorithm always works.
*/
Let s, t be a maximally distant pair. Let u be the arbitrary vertex. We have a schematic like
u
|
|
|
x
/ \
/ \
/ \
s t
where x is the junction of s, t, u (i.e. the unique vertex that lies on each of the three paths between these vertices)./*
At this point any leaf v of u, of maximum distance from u, is selected. We only need to show that a path of maximum length can be built with v as an end point. If v lies on any of the paths u --- x, x –-- s or x –-- t then it must be s or t (otherwise it wouldn’t be of maximum distance from u).
In that case s --- t is a maximum path where one of its endpoints is v. So, now we only need to consider the case where v doesn’t belong to any of the three paths shown in the schematic. In that case, v must be below a node in x --- s or x --- t or u --- x (but not s or t because s --- t has maximum length).
*/
Suppose that v is a vertex maximally distant from u. If the schematic now looks like
u
|
|
|
x v
/ \ /
/ *
/ \
s t
then
d(s, t) = d(s, x) + d(x, t) <= d(s, x) + d(x, v) = d(s, v),
where the inequality holds because d(u, t) = d(u, x) + d(x, t) and d(u, v) = d(u, x) + d(x, v).
There is a symmetric case where v attaches between s and x instead of between x and t./*
Note that d(x, t) <= d(x, v) because otherwise the path u --- t would be larger than u --- v, but v has maximum distant from u. So, d(s, t) <= d(s, v) implies that the path s --- v has maximum length
*/
The other case looks like
u
|
*---v
|
x
/ \
/ \
/ \
s t
Now,
d(u, s) <= d(u, v) <= d(u, x) + d(x, v)
d(u, t) <= d(u, v) <= d(u, x) + d(x, v)/*
Let’s call these inequalities the “base” inequalities, for future reference. The goal is to find a path starting with v whose distance is >= d(s, t). So, we want to find an inequality <= with d(s, t) on the left side and v on the right
For the first inequality
d(u, s) <= d(u, v) holds because v has maximum distance from u
d(u, v) <= d(u, x) + d(x, v) holds because x is below * (so path re-tracing occurs)
The second inequality holds by the same reasoning
*/
d(s, t) = d(s, x) + d(x, t)
= d(u, s) + d(u, t) - 2 d(u, x)
<= 2 d(x, v)/*
Let’s call the inequality at the bottom the “derived” inequality, where d(s, t) is on the left side. The second equality holds because
d(s, x) = d(u, s) - d(u, x)
and
d(x, t) = d(u, t) - d(u, x)
The inequality below it holds because of the base inequalities
d(u, s) <= d(u, x) + d(x, v)
d(u, t) <= d(u, x) + d(x, v)
*/
2 d(s, t) <= d(s, t) + 2 d(x, v)
= d(s, x) + d(x, v) + d(v, x) + d(x, t)
= d(v, s) + d(v, t)
so max(d(v, s), d(v, t)) >= d(s, t) by an averaging argument, and v belongs to a maximally distant pair./*
The inequality at the top holds because of the derived inequality
d(s, t) <= 2 d(x, v) so 2 d(s, t) <= d(s, t) + 2 d(x, v)
The equality below it follows because
d(s, t) = d(s, x) + d(x, t)
and
2 d(x, v) = d(x, v) + d(v, x)
The last equality holds because:
d(s, x) + d(x, v) = d(v, s)
and
d(v, x) + d(x, t) = d(v, t)
The conclusion follows because at least one of d(v, s) and d(v, t) must be >= d(s, t) if their sum is >= 2 d(s, t)
*/
References
[1] “Proof of correctness: Algorithm for diameter of a tree in graph theory”, 2018, David Eisenstat, Google


