Bitmasking and bitwise

operations are low level programming techniques used for turning bits off and

on - the manipulation of bits provides a way to make representations in a

computer. The goal of bitmasking in SQL Server 2005 is to combine two or more

attributes, normally stored into a single column in a table, into one

hexadecimal value to make representations as well. Achieving this goal has many

possibilities, as we will discover later, and introduces many computer science

concepts into the relational database. Part 1 of this series is an introduction

to counting and bitmasking in SQL Server. In Part 2, we will discover its

practical application in SQL Server. Finally, in Part 3, we will explore

programmability using bitmasking techniques.

Why Bitmask?

Suppose,

for instance, that you have been assigned to capture 50 Request.Browser

properties (Figure 1) from your website and maybe 50 keys in the Request.ServerVariables

collection off of the web to store in SQL Server. Are you going to create 100

columns in a table to hold these values? Sure, you can and that will work very

well, but bitmasking several values to one value is a cleaner, neater, and more

efficient approach in my opinion.

Figure 1 : A Request.Browser property (c#)

Figure 1 shows one of many

different attributes that you can pluck out of a user's visit to a website,

important information that many companies capture. Here, a web developer writes

code to capture the Boolean value of a browser's cookie status. Before we get

into an example, we must review numbers, counting, base 10, base 2, and

hexadecimal notation.

(If you are already familiar

with these concepts, please skip this part). You will need to understand these

terms and associated techniques to begin masking multiple values to single

values.

A Review of Bits, Numbers and Counting

The basic and lowest level

of a computer's representation of anything is a bit. A bit has two values as

most of us know on and off. While you expected me to say 1 and 0, one only

has to look at a half a dozen different ANSI applications to find that on and

off are represented a half dozen different ways. For this article, we will use

0 and 1; don't be surprised, however, to find other values, highly inconsistent

might I add, even in platforms and applications that are written by the same

company, no less. Generally speaking, we associate 1 to be equal to on; 0 to

represent off, but if you wanted to you could reverse this representation I

suppose. Table 1 defines a table for some of our terminology. Four bits are a

nibble and two nibbles are a byte. A WORD is 2 bytes, or 16 bits, and 32 bits

are a DWORD. A nibble will be a very important term to grasp as we begin

mapping bits.

Table 1 :Bit terminology

Numbers can be represented

via a series of bits in combinations that are either on or off. Your computer

represents things as numbers as well, such as memory locations, printer ports,

devices, etc. When you think about it in this context, we can certainly represent

things with numbers of our choosing if we are inclined to in the relational

database - permissions, cities, states, hair color, gender can be assigned a

numerical value. And by doing such, we are representing entities, objects,

or things just as your computer does. Let us now look at Base 10 and Base 2

notation. This will allow us to become acquainted with numbers and their

representations. We'll first pick an easy number, and then a larger one as our

working examples. If you remember from mathematics, our numbering system is centered

on the Decimal System, or Base 10. Let's look at some Base 10 representations

of our numbering system. Understanding the following is critical to bitmasking

in SQL Server 2005.

Base 10

Check out Table 2 for a

refresher on simple Base 10 counting. We will build off of this concept later. Remember

that we can count numbers in a variety of ways. Follow each line in the

graphical representation to get (re)acquainted with counting numbers in this

manner. At this point, a calculator might be handy to verify some of what I am

deriving.

Table 2 : Counting numbers with Base 10

We certainly could have expanded line 11 in our table even further, but I think you get the point. The number 10 is the base value of our final calculation here, and we can express final results based on 10 raised to a power times another value.

Base 2

As Base 10 is synonymous with the Decimal system, so is Base 2 to the Binary System.

Because bits are used to represent numbers in a computer, we find it easier to translate our numbering to bit notation (we previously pointed out that the core of computing is based on only two values). Rather than using Base 10, we will use a Base 2, as it provides to us a much easier way to represent our values.

A very important concept, Base 2 allows us to translate from hexadecimal to decimal and back very easily. Mapping values using base two is much easier than trying to keep up with counting all of the zeroes and ones when using Base 10.

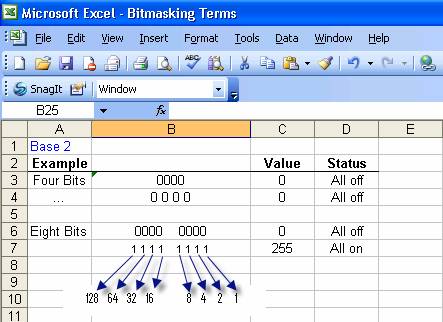
Table 3 : Base2 mapping

The above table first shows us that one nibble and one byte, all zeros, has a value of zero. A byte, all 1's (all bits turned on) has a value of 255. How did we come up with this?

Let's break this down piece

by piece. Don't worry all of this will come together for you soon. Each bit

position represents an ordinal position within a byte. Starting from right to left

(we could have started from left to right it's personal preference), position

0 is represented by two to the zero power, which equals one. Moving to the left

one position, we find two to the first power, or 2^ 1, which gives us the value

of two. (Notice the increasing value of the exponent by one, starting at zero, each

iteration). Again using base two, our Base 2 value next is raised to the

second power, and then two raised to the third power, etc. Since all the bits

are on in the first nibble of this byte, what is the value of the sum of the

first four numbers? Fifteen, you are correct!

Now let's examine our value

of 15 further, and place it in our windows scientific calculator. Make sure

that you enter 15 and that it is reading in Dec, short for decimal notation.

Now, change it to Hex, short for Hexadecimal notation. What the heck? Our value

is F. Where did this come from? Remember that our visual representation is

easily changed to Hex from Base 2.

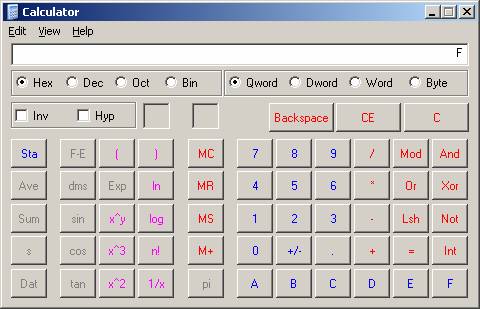
Display 1 : Our value 15 as Hexadecimal

Review Table 4. This mapping allows us to successfully convert our numbering scheme from base two to Hex notation. This final representation of numbers is what we will actually use in our masking far easier than trying to convert base 10 or base 2 to something visual that we can work with.

Table 4 : A conversion table for bits

Study this concept for a moment, and try to come up with some values of your own. For practice, jot down a few numbers between 0 and 20 and try to figure out their binary value

representation.

Let's look at another example, this one is more difficult. Let's attempt to map the hex value of our previous, 4458. Before we can do this, we have to calculate its value in Base2. We must first figure out how to get there. Here is what I come up with:

If we now map each nibble, we end up with the following:

Notice how each set of 4 bits translates nicely into our first beginning value of Base2 exponential notation. Let's look at it again:

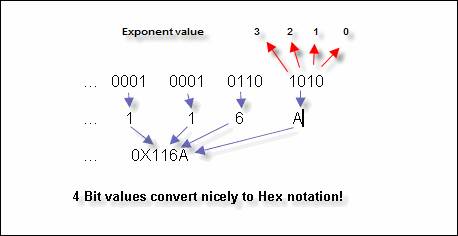
We treat each nibble as if they were stand alone the first nibble is the sum of 2 + 8, since the second and forth bits are on, giving us a value of 10 (or the value A!). For the second nibble, the second and third bits are on, summing to give a value of.6(2 + 4). Yes you got it! Revisiting our scientific calculator, we see that our numbers appear to be correct.

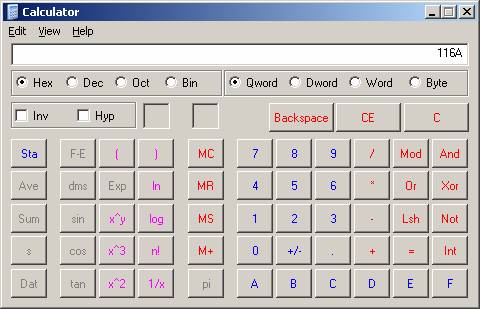
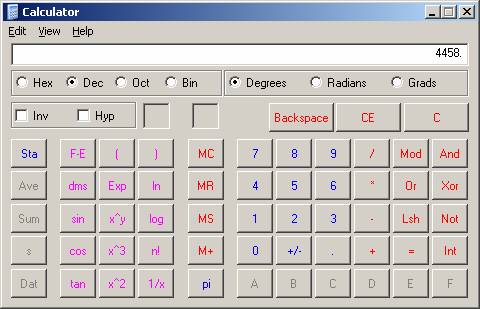
Display 2 : Our number 4458 as Hex and Dec

Again, review this concept carefully before moving on. Pick a few numbers larger than, say, 100, and come up with 1) its binary representation and 2) its hex representation. Understanding this exercise, converting from decimal to binary to hexadecimal, is critical to successful bitmasking. Let's now begin with a fictitious problem and solve it via bitmasking.

Our Problem

Given

our refresher, we are ready for a challenge. We have been tasked to bitmask 3

values that are generated each time a visitor comes to our website. We are to

record 1) the operating system, 2) the browser used, and 3) whether or not

cookies are turned on in the client environment. We wish to combine these three

values into 1 bitmasked value and store this in the database.

Preparing to code our mask

Before

we begin coding T-SQL, I first find it easy to mask values into a single value

by creating a key, or legend, that will guide me to the correct bit placement

of my values. Below is a useful way to prepare a legend as a map to 1) Define the

number of bytes needed, 2) Keep track/calculate bit values, and 3) Position of

the bytes where you wish to store your values. Simply add one of these as a

comment in your code so that you have a reference to go back whenever you like

to remind yourself of the mask positions for your values. Examine the key in

Figure 1 and study the explanation of the key carefully.

Figure 2 : Creating a key to map bitmask values

Explanation of the key

In our example, we will use only 1 byte to represent three columns. (If you were masking several columns, you

would need more bytes for storage). First, I assign the placeholders for the

bit values: 2 bits for the operating system, 3 bits for the browser type, and 1

bit to notify if cookies are turned on or off. The second portion of the key

outlines the assignment for your mask. We are using 1 byte which has 8 bit

positions. Each position will be assigned bit values. For O (operating

system), I previously defined in the key that we will allow three values, so

I'll need 2 bytes. For Browser B storage, I'll need 3 bits (Remember why 3

bits allows for 7 storage values? If you forgot, go back and review counting

numbers. You'll get it!), and for Cookie C values just 1 bit. Note that I map

them in the Mask line above, each of the 6 bits that I'm using assigned to a

corresponding value for my mask. This is very important, since you will actually

be placing numerical representations of your data within these bits. It does

not matter than I do not use all 8 bits that I have allocated in our example

we can leave the remaining bits zero without disrupting our storage or

retrieval process.

Coding the Mask

Below is the code that will mask our values. Review this script, and then look a the explanation below.

Figure 3 : Code to mask our data into one value

Lets briefly review the above steps for coding the mask.

Steps to mask values

Step 1) Binary data type

at this point, you choose the binary or varbinary data type that you will use.

The more values that you have, the larger the data type necessary to store

values. I use a varbinary (1) data type for no reason other than I normally use varbinary instead of binary (length 1 doesn't vary, obviously).

Step 2) Assign Mask Values values that we wish to mask. They could come from

a web page, a rich client, web service, or whatever. For this initial demo, we're

just running a script, so hard-coded values are adequate.

Step 3) Assign the shift values these variables store the multiplier to allow

you to shift, within the byte or bytes, the beginning point for you storage

attributes. For example, the first variable, @BitshiftBrowser=4, will allow us to skip the first two bits (our

designated holding spot for the operating system) in order to get to the location

where we are going to store our browser settings.

Step 4) Assign code to values in order to store our values, remember back to

our previous paragraph on object representations in the computer. Here we

simply assign a number to our value via the CASE

statement.

Step 5) Mask the values use the bitwise OR operator to place the integer

value that represents our textual value inside of the binary data type at the

outlined location. (For further reading, see http://en.wikipedia.org/wiki/Bitwise_OR#OR).

Step 6) Masked value our end result. We have successfully collapsed 3 attributes into 1 value (Figure 3); we could have put hundreds of them into one value. A powerful concept? I agree!

Figure 4 :Bitmasked value final result

Decoding the Mask

Just as we code the mask, similarly we must decode the hexadecimal value (Figure 5). Let's look at the steps to accomplish this.

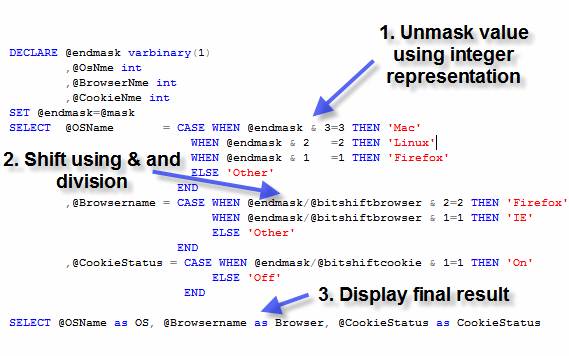
Figure 5 : Decode the masked value

Steps to decode mask values

Step 1) Unmask value using

integer representation This is a simple decode. The values that you

previously assigned to your textual representation are reversed. For the first

bit, you perform a bitwise AND (http://en.wikipedia.org/wiki/Bitwise_AND#AND)

to recapture the values.

Step 2) Shift using & and division As we shifted to the right to place the

values into the mask, we must divide by the same bitshift variable to decode

the second and subsequent values out of the mask. The mask value/shift integer anded

with the storage value assigned in the code mask steps is found again by the CASE statement.

Step 3) Display final result

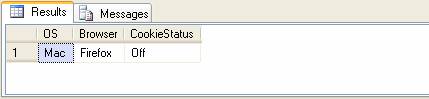
Figure 6 : Final decoded value

Conclusion

Bitmasking in SQL Server is fun, powerful, and a neat way to store data in a relational database. While it shouldn't be used to overpower or overcomplicate solving a particular task, as it is with every tool in our SQL Server toolkit arsenal, there is a time and a place for everything. Keep this technique in mind next time you have to store many attributes into a table. In Part 2, we will look at how you might build objects in the database that will allow implementation of this concept. We'll also look at some queries and indexing the bitmasked value, and look at performance implications for a bitmasked value in SQL Server.

About the Author

Lee Everest is a Sr. Consultant for Software Architects, and a part-time SQL instructor at North Lake College in Irving, Texas. He can be reached at tsql-northlake@dcccd.edu