Introduction

Sometimes, the only way to know if the code that you've written or the index that you've built will perform and scale well is to test it against large amounts of data. On new projects in particular, such quantities of data aren't always available. One way to build such data is with commercial data generators such as Red Gate's SQL Data Generator 2.0 software.

But what if you don't have such a tool?

This series of articles will show you how to quickly build test data. In Part 1, we'll learn how to generate and control the domains of large quantities of random integers and floating point numbers (the foundations of many types of test data) in a very high speed fashion. In Part 2, we'll learn how to convert those fundamental values to other types of test data such as dates, currency amounts, alphanumeric department numbers, and even random-length simulated names.

None of the methods used in either of these articles are new. In fact, methods similar to those found in this article form the very foundation of many of the commercial data generators. The difference is that we're going to use T-SQL to generate the data and it'll all be done without using While loops or any other form of RBAR¹. If you didn't know you could easily and quickly (a million rows in just several seconds) generate vast quantities of meaningful test data using just a small bit of T-SQL or you just want to know more about how it can be done, then this series is for you.

For those with the question, yes. Except for a couple of ROW_NUMBER() OVER examples, all of the random number generation methods will work as far back as SQL Server 2000. They may work in 6.5 and 7 but I've simply not tested that far back.

Special thanks goes out to Peter Larsson, Michael Valentine Jones, Matt Miller, R.Barry Young, Andy Dowswell, and a host of others for their contributions on this subject over the years. I also thank Wayne Sheffield, Ron McCullough, and Craig T. Farrell for providing some wonderful suggestions during their review of this article.

The Basic Formulas

Many types of test data can be generated either from constrained random integers or random floating point numbers. While several different methods exist for the creation of such numbers, there are two basic formulas in particular that will allow us to generate large quantities of said numbers in a high performance, set-based fashion in T-SQL.

The following code generates a million rows of random integers (the SomeRandomInteger column) with possible values from 400 to 500 and float values (the SomeRandomFloat column) from 400 to 500.999999999999 in just over 4 seconds on my 10 year old, single CPU computer. The code will run much faster on more modern computers.

--===== Declare some obviously named variables
DECLARE @NumberOfRows INT,
        @StartValue   INT,
        @EndValue     INT,
        @Range        INT
;
--===== Preset the variables to known values
 SELECT @NumberOfRows = 1000000,
        @StartValue   = 400,
        @EndValue     = 500,
        @Range        = @EndValue - @StartValue + 1
;
--===== Conditionally drop the test table to make reruns easier in SSMS
     IF OBJECT_ID('tempdb..#SomeTestTable','U') IS NOT NULL
        DROP TABLE #SomeTestTable
;
--===== Create the test table with "random constrained" integers and floats
     -- within the parameters identified in the variables above.
 SELECT TOP (@NumberOfRows)
        SomeRandomInteger =  ABS(CHECKSUM(NEWID())) % @Range + @StartValue,
        SomeRandomFloat   = RAND(CHECKSUM(NEWID())) * @Range + @StartValue
   INTO #SomeTestTable
   FROM sys.all_columns ac1
  CROSS JOIN sys.all_columns ac2
;

Most of that code is in the form of variable declarations and presets. The code we'll spend most of our time on in this article can be isolated to just the following snippet of code.

--===== Create the test table with "random constrained" integers and floats
     -- within the parameters identified in the variables above.
 SELECT TOP (@NumberOfRows)
        SomeRandomInteger =  ABS(CHECKSUM(NEWID())) % @Range + @StartValue,
        SomeRandomFloat   = RAND(CHECKSUM(NEWID())) * @Range + @StartValue
   INTO #SomeTestTable
   FROM sys.all_columns ac1
  CROSS JOIN sys.all_columns ac2
;

There are several important things to note about the code.

1. All ¹RBAR has been avoided. There is no Cursor, While loop, or recursive CTE in the code, which allows it to run at incredible speed.
2. The random integer and float formulas are very similar to each other and easy to remember.
3. The code is remarkably short for what it does.
4. All variables can easily be replaced with constants, which means that this is really all of the code we need.

Let's break the code down and see how it all works.

Generating Rows

Before we can talk about how to generate lots of test data, we must first figure out a way to quickly generate a lot of rows. Yes, you could use a WHILE loop or a "Counting Recursive CTE", but there are much quicker and simpler methods, in most cases. Let's explore the method used in this article.

FROM – Avoiding the Loop

The code selects from a system view called "sys.all_columns". If you look at the code carefully, nothing from that view is actually selected. So what does selecting from the view (and it could be any view or table) actually do for us?

Simply stated, it loops. I use to call it a "set based" loop until R.Barry Young coined the phrase "Pseudo Cursor", which is what I call it now but, behind the scenes, it's still a loop. For each iteration of the loop, it builds a new row for us… and it's nasty-fast.

To understand how it all works, let's run through some simple questions and examples. Experienced users may actually find the questions and answers a bit insulting in their simplicity and nature but I certainly don't mean for them to be so. I just want to make sure that even a beginner to T-SQL understands exactly what is going on and why, so please bear with me.

Question #1: What does the following code do?

 SELECT *
   FROM sys.all_columns
;

BWAA-HAAA!!! Yes, I absolutely agree! The "SELECT *" offends most folk's sensibilities as to what efficient code is. Think simpler.

Yep. You're getting warmer. It does, in fact, return all of the columns of the view. That's not what I'm looking for though. Think even simpler. What else does it do?

Correct! Because it doesn't have a WHERE or TOP clause, it returns all of the rows from the view.

Here's question number 2.

TOP – Limiting the Number of Rows

Question #2: Given that the view used in the following code has more than 4,000 thousand rows in it, what does the following code do? (Hint: Think about the answer to the previous question)

 SELECT TOP (1000)
        *
   FROM sys.all_columns
;

Now I'll just bet that everyone got that right the first time. Correct! It returns the 1,000 rows from the view. Which 1,000 rows does it return? Without an ORDER BY, it's really impossible to tell but you're also getting ready to find out that it doesn't matter for what we eventually want to do.

What is the code actually doing though? Do those rows just magically pop onto the screen?

No. If you had a much larger table or view and SSMS was in the "Results as Text" mode, you'd see that the rows are returned one at a time. Behind the scenes, SQL Server does what every decent file process does. To over-simplify, it finds the "first" row, reads the row, displays the row, determines if it has displayed all the rows it needs to, and loops back to find and display the next row until done. Yep! SQL Server loops like crazy behind the scenes for queries that return more than one row.

R. Barry Young referred to that "behind-the-scenes" looping as a "Pseudo-Cursor".

Question #3: Given that the view used has more than 4,000 rows in it, what does the following do?

 SELECT TOP (1000)
        1
   FROM sys.all_columns
;

Since there are more than 1,000 rows in the table, the code will return one thousand "1"s. An important point to observe here is that we didn't actually use any of the data from the table. We only used the "presence of rows" from the table to generate 1,000 ones.

Let's kick things up a notch.

Building Variable Content Rows (Sequential Numbers, in this case)

Question #4: Given that the view used has more than 4,000 rows in it, what does the following do?

 SELECT TOP (1000)
        ROW_NUMBER() OVER (ORDER BY (SELECT NULL))
   FROM sys.all_columns
;

If you've never seen such a thing before, take the time to run the code above on your own machine. What you'll find out is that the code sequentially generates all integers from 1 to 1,000. Because the OVER clause won't allow a constant in the ORDER BY, SELECT NULL was used to make the ORDER BY work. To emphasize again, this means that we didn't actually use any of the data in the table. We just used the "presence of rows" to "loop" through a thousand rows and we generated 1,000 rows of data (a simple sequence of integers, in this case) from that action.

The problem is that the view being used only has a little over 4,000 rows in it. How could we generate, say, a million rows without having a million row table or view to draw from?

CROSS JOIN – Building Large Numbers of Rows

Question #5: Given that the table used has at least 4,000 rows in it, what does the following do?

(WARNING! Don't actually run this code because it will try to build a huge number of rows that can run your system out of memory!)

 SELECT ROW_NUMBER() OVER (ORDER BY (SELECT NULL))
   FROM sys.all_columns ac1
  CROSS JOIN sys.all_columns ac2
;

A CROSS JOIN builds what is known as a "Cartesian Product". In other words, it builds a "double loop" where the rows in the first view are scanned once for every row in the second view. In this case, we used the same view with at least 4,000 rows in it, twice. So, the code will scan through all 4,000+ rows in the "first" view (aliased as "ac1") once for every row in the "second" view (aliased as "ac2"). Since there are at least 4,000 rows in the view, we'll scan through 4,000 * 4,000 rows for a total of at least 16 MILLION rows (more since the view has more than 4,000 rows).

So the answer to Question #5 is that the code will count from 1 to at least 16,000,000 returning a row for each count.

Of course, if we only want a million rows, we can put a "cap" on the number of rows returned just like we would anywhere else…

 SELECT TOP (1000000)
        ROW_NUMBER() OVER (ORDER BY (SELECT NULL))
   FROM sys.all_columns ac1
  CROSS JOIN sys.all_columns ac2
;

So not only is it possible to generate many more rows than your largest table or view has, it's also quite simple. We only used a total of 4 lines of code and two of them are near duplicates of each other. Try that with a WHILE loop!

Again, we never used any of the data from the table. We only used the "presence of rows" which formed a very high speed Pseudo Cursor (a nested loop, in this case… see the execution plan) behind the scenes and that eliminates the need for a much slower explicit loop or the hidden RBAR¹ of a "counting rCTE". Why is that important? Just one reason… blinding speed.

Summary of Building Rows

To summarize this section of the article, we've seen that the CROSS JOIN on a particular table or view can provide millions of rows even if we don't actually use anything from the table or view we've cross joined. We've seen that we can use a formula that will make use of the "presence of rows" and generate its own data instead of using data from the table or view itself. And we've also seen that we can use TOP() to control the number of rows that we generate.

We still don’t have anything truly useful for building randomized data but we have seen how to generate a large number of rows that each contains something different.

As a bit of a sidebar, if you'd rather not use a system table or view to generate rows, you could always build a "Tally" table to use as a known row source. Please see the article at the following link for what a "Tally" table is, how to build one, and how it can be used to replace certain WHILE loops.

http://www.sqlservercentral.com/articles/T-SQL/62867/

INTO

Instead of having to write the code to first build a test table and then populate it, we can do both at the same time. The "INTO" is actually a part of what is known as a "SELECT/INTO". The SELECT acts as you would expect any SELECT to act. The "INTO" part determines the data-type and NULLability of the columns it builds from the Select List (the formulas being selected) and builds a table from it. If the table already exists, it will throw an error so you probably need to conditionally drop the test table at the beginning of the run.

There are three huge advantages to using SELECT/INTO over first building the test table and then populating it. The first is that you don't have to write as much code. The second is that if the database that holds the test table is in the BULK LOGGED or SIMPLE recovery mode (TempDB is always in the SIMPLE recovery mode), SELECT/INTO will perform a "minimally logged" operation. Minimally Logged operations don't record the actual rows you've made in the new table, which means that your log file probably won't grow even when creating millions of rows of test data. The third is blazing speed even if it turns out to not be a minimally logged operation.

For more information on the "Minimally logged" aspect of SELECT/INTO, please see the "Logging Behavior" section and Example "B" of the following link. See the link that follows that for more information on other "Minimally logged" operations that SQL Server can perform.

http://msdn.microsoft.com/en-us/library/ms188029.aspx
http://msdn.microsoft.com/en-us/library/ms191244.aspx

Yes, it's true that SELECT/INTO does put some locks on system tables during its operation. But the code runs super fast and the locks don't actually prevent new tables from being formed in TempDB. Please see the following Microsoft Article on the "myth" that SELECT/INTO cripples a server while it's running.

http://support.microsoft.com/kb/153441/EN-US/

I have "myth" in parenthesis because it will cripple (long term exclusive locks) the source of information if you use it across a Linked Server.

The Problem with RAND()

The first thing that most of us think of when it comes to generating test data is "random data". Of course, the next thing we think of is something to generate random values with and, in SQL Server, our thoughts immediately turn to RAND() which generates random FLOAT values from 0 up to and not including 1.

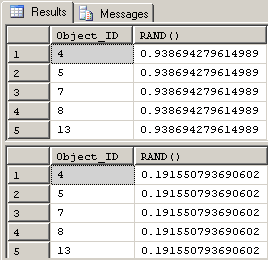
Although RAND() will return a different random float each time you run a query containing RAND(), any and all rows in that query will produce the exact same value for RAND() for any given run. Try it. Here's a query that will generate 5 different rows (proven by Object_ID) but all values of RAND() are identical for each row. Each time you run the query (I used "GO 2" to run it twice), the value of RAND() will change but it will still produce the same number for the value of RAND() for all rows returned in a run.

 SELECT TOP (5)
        Object_ID,
        [RAND()] = RAND()
   FROM sys.all_objects
;
GO 2

Here are the results on my machine for the code above. Your results stand a pretty good chance of having different values for the RAND() column, but the results within a given result set will all be the same.

Because RAND() (the unseeded and fixed seed versions) can only be different for separate queries, you might be tempted to force RAND() to change values by using a WHILE loop to make many different inserts. Let's create a WHILE loop to build a million row table with different values of RAND() as an example for comparison.

--===== Conditionally drop and rebuild the test table
     -- to make reruns easier.
     IF OBJECT_ID('tempdb..#TestTable','U') IS NOT NULL
        DROP TABlE #TestTable;
GO
 CREATE TABLE #TestTable
        (RandomNumber FLOAT);
--===== Suppress the auto-display of row counts to
     -- speed things up
    SET NOCOUNT ON;
--===== Create a million random numbers and insert
     -- them into the table one at a time.
DECLARE @Counter INT;
 SELECT @Counter = 1;
  WHILE @Counter <= 1000000
  BEGIN --===== Insert a random value
         INSERT INTO #TestTable
                (RandomNumber)
         SELECT RAND();
        --===== Increment the counter
         SELECT @Counter = @Counter + 1
    END;

That took exactly 1 minute to run on my humble, circa 2002, single CPU desktop. Of course, it'll run much faster (about 22 seconds) on newer machines but it'll still take a fair bit of time… more time than most people need to wait in either case. Discounting the code to conditionally drop and build the test table, it also took a fair bit of code to accomplish. You'll waste even more time if you forget to SET NOCOUNT ON because it takes a lot of time (about 50% more) to print a million row-counts of 1.

And, we haven't even generated any useful test data, yet.

So, the direct use of RAND() without a seed or with a fixed seed won't work the way we'd expect it to unless we use a WHILE loop to make separate inserts with. How are we going to quickly generate random numbers without a loop?

NEWID() – A Random Generator

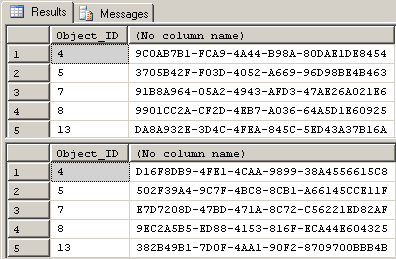
There IS another source of random data. Microsoft currently uses "Type 4" GUIDs (or UUIDs, if you prefer) for the NEWID() function. A "Type 4" GUID isn't much more than a random value ("Pseudo-Random" value if you care to research the difference). By itself, it's almost as useless a random value as the output of RAND(), but at least it will produce a different random value no matter how many rows a query containing NEWID() returns. Try it and see… 

 SELECT TOP (5)
        Object_ID, NEWID()
   FROM sys.all_objects
;
GO 2

Here are the results when I ran the code above. As you can see, the values of NEWID() are quite random even in the same run.

Because it returns a different value for each row returned even in the same query, it also lends itself to eliminating the WHILE loop and enabling us to build the test table on-the-fly in a very high speed manner using SELECT/INTO. Further, the code to do it all is a lot shorter than the WHILE loop method. Try it on a million rows and see… 

--===== Conditionally drop and rebuild the test table
     -- to make reruns easier.
     IF OBJECT_ID('tempdb..#TestTable','U') IS NOT NULL
        DROP TABlE #TestTable;
GO
--===== Generate a million random values
 SELECT TOP 1000000
        RandomValue = NEWID()
   INTO #TestTable
   FROM sys.all_columns ac1
  CROSS JOIN sys.all_columns ac2;

That bit of code took 1.5 seconds even on my old war-horse of a machine. The values we stored are still useless as test data, but at least we've stored a million rows of something random in a whole lot less time than the WHILE loop. We also don't have to worry about making sure that we SET NOCOUNT ON. In fact, we now get verification that we inserted a million rows in the form of a single row-count.

Still, the output of both RAND() and NEWID() hardly constitute meaningful test data. Let's begin the transformation of such "data" to more meaningful test data.

CHECKSUM() – A Quick Converter

Even random float data needs to start out with random integers. Why? Because in perhaps the most ironic twist of fate there is, RAND() in T-SQL requires a random seed to produce different random numbers within a given query. According to Books Online, that random seed must be something that can be implicitly converted to an INT. NEWID() can't be implicitly or explicitly converted to an INT. You can convert NEWID() to a VARBINARY() as a first step in the conversion process and then convert that to an INT, but that also takes some extra processing time.

Enter CHECKSUM().

CHECKSUM () will convert just about anything to a hashcode (a integer calculated using a type of checksum). If you give it a random value, such as a NEWID(), it will create a random hashcode and it does so very quickly. What's really neat about all of this is the hashcode is an INTEGER so there's no need for an additional conversion. Let's see it in action.

--===== Conditionally drop and rebuild the test table
     -- to make reruns easier.
     IF OBJECT_ID('tempdb..#TestTable','U') IS NOT NULL
        DROP TABlE #TestTable;
GO
--===== Generate a million random Integers using CHECKSUM(NEWID())
 SELECT TOP 1000000
        RandomInteger = CHECKSUM(NEWID())
   INTO #TestTable
   FROM sys.all_columns ac1
  CROSS JOIN sys.all_columns ac2
;

That code took 1.5 seconds on my old machine. It's virtually the same speed that NEWID() took by itself and we now have random integers instead of GUIDs. Granted, the integers are still useless as they are because they're all over the place (including negative integers) and don't fit anything we might need, but they are random integers.

Here are what the top 10 rows of the test table looked like after I ran that code.

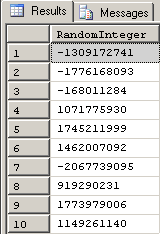
Again and still, the random numbers we have are pretty useless as test data because we don't actually have any control over what the min and max values (the limits) of the random numbers might be. In order to apply such limits, we need to learn about some random number math. First, let's convert the negative values to positive values.

ABS() – All Things Positive

This is where the two random number generator formulas begin to differ from each other a bit. For random integers, we normally work with random positive integers and zero. So, the first step would be to change all of the random integers we previously built to positive integers.

Without getting into a discussion on "Number Lines" and what it all really means, the ABS() function (ABS stands for ABSolute Value) will convert negative integers to positive integers. Let's apply that to what we have so far.

--===== Conditionally drop and rebuild the test table
     -- to make reruns easier.
     IF OBJECT_ID('tempdb..#TestTable','U') IS NOT NULL
        DROP TABlE #TestTable;
GO
--===== Generate a million random positive Integers using ABS(CHECKSUM(NEWID()))
 SELECT TOP 1000000
        RandomNumber = ABS(CHECKSUM(NEWID()))
   INTO #TestTable
   FROM sys.all_columns ac1
  CROSS JOIN sys.all_columns ac2
;

Here are what the first 10 rows of that code looked like on my machine. Notice that we only have positive integers, now.

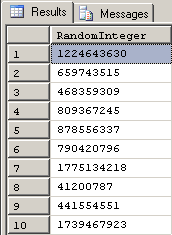
That ran in just a bit over 1.5 seconds on my machine. The ABSolute conversion didn't take much time at all. Still, we have some basically useless positive integers because they're so wildly spread. We'll fix that later in this article but let's see what the float side of the world looks like, first.

RAND() – Random Float Values

RAND() will also convert negative and positive integers to just zero or positive values. But, just in case you don't know, it doesn't return integers and it only returns a very narrow range of floating point values. In fact, the only values it returns are greater than or equal to 0 and less than 1. For the mathematicians in the house, the formula for the numbers returned by RAND() can be expressed as "0 <= X < 1".

If we use CHECKSUM(NEWID()) as a random seed for RAND(), we end up with the following code.

--===== Conditionally drop and rebuild the test table
     -- to make reruns easier.
     IF OBJECT_ID('tempdb..#TestTable','U') IS NOT NULL
        DROP TABlE #TestTable;
GO
--===== Generate a million random positive Floats from 0 to less than 1
 SELECT TOP 1000000
        SomeRandomFloat  = RAND(CHECKSUM(NEWID()))
   INTO #TestTable
   FROM sys.all_columns ac1
  CROSS JOIN sys.all_columns ac2
;

Here are what the first 10 rows of that code returns.

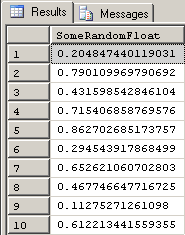
Once again, that's clever and nice but the numbers are still basically useless as test data in their current form. We need to convert the numbers to something more useful. We'll do that by defining and using some "limits".

@Range - Establishing the "Limits"

Let's take a look at just the formula lines in our random number generators…

SomeRandomInteger = ABS(CHECKSUM(NEWID())) % @Range + @StartValue
SomeRandomFloat = RAND(CHECKSUM(NEWID())) * @Range + @StartValue

The only real difference between the two formulas is a single function and a single mathematical operator. In both cases, we've already learned that CHECKSUM(NEWID()) will produce a random integer somewhere between the most negative and most positive extents of the INT data-type. Those random integers are mostly useless as they are because they have too wide a range. For example, if we want random integers from 1 to 5, values such as minus 84759284 aren't going to be very helpful as they are. We have to somehow limit the random integers to values of 1 through 5. In order to do that, we first need to understand a little about "ranges".

In the two random data formulas above, we see that both have an @Range variable. Again, using the example of creating random numbers from 1 to 5, let's see what that variable should contain.

I know it sounds silly, but count from 1 to 5 on your fingers and ask yourself how many fingers you just counted. The answer is, of course, 5. This also means that there are 5 unique numbers from 1 to 5.

Ok, same problem but with a wider range of numbers. How many unique numbers are there from 400 to 500?

Some people will quickly do the math of subtracting 400 from 500 and say that there are 100 unique numbers. In fact, there are 101 unique numbers from 400 to 500 inclusive.

We've already determined that there are 5 unique numbers when counting from 1 to 5. In order to determine the number of unique values, we need to subtract 1 from 5 and that gives us the answer of 4. Because of the subtraction, we need to add 1 to come up with the correct number of unique values.

The same holds true for determining the number of unique values from 400 to 500. We subtract 400 from 500 and then add 1 just like we did for the 1 thru 5 problem. There are 100 unique numbers from 401 to 500 and then we have to add 1 to include the number 400.

We haven't yet explained how it will be used to limit the values of our random number generators but the formula for determining the value of @Range for both the random integer and random float formulas is as follows:

--===== The "Inclusive Range" Formula
 SELECT @Range = @EndValue - @StartValue + 1;

% - The Modulo Operator – Applying the "Limit" for Random Integers

Let's have another look at the random integer formula.

SomeRandomInteger = ABS(CHECKSUM(NEWID())) % @Range + @StartValue

As we've already discussed, the ABS(CHECKSUM(NEWID())) generates an integer that's greater than or equal to 0. How can we limit the values it returns to 1 thru 5, for example? We've already seen that we'd use a "5" for @Range but how does that provide a limit for our random integer generator?

As you can see, there's a "%" symbol being used as a mathematical operator in association with @Range. That's the "Modulo" operator. MODULO simply returns the REMAINDER of integer division.

Let's see how it works and how it acts as a "limit" on our random number generator.

The first column in the graphic below contains a list of numbers from 0 to 15. The second column contains the Divisor of 5. The third column contains the integer result or Quotient of the integer division. The fourth column (the Yellow one), contains the Remainder of the "Integer Division". Do you notice a pattern in that fourth column?

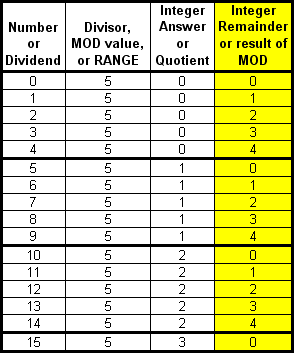
The Remainder not only repeats itself, but it always starts at zero and the largest Remainder (4, in this case) is ALWAYS exactly one less than the Divisor (5, in this case)

As previously stated, MODULO simply calculates the Remainder of integer division. For integers greater than or equal to zero, here are the simple rules for remainders and, thus, for MODULO.

1. The lowest possible remainder returned will always be 0.
2. The highest possible remainder returned will always be 1 less than Divisor. The MODULO number or "Range" number is nothing more than a Divisor.
3. The number of unique integer values that can possibly be returned as Remainders by integer division of positive integers will always be equal to the value of the Divisor. MODULO only returns remainders of integer division.

How does that apply to our problem of generating random integers from 1 to 5? Here's a similar chart of numbers as above but, instead of having orderly numbers from 0 to 15, we have 16 random integers that were generated by ABS(CHECKSUM(NEWID())).

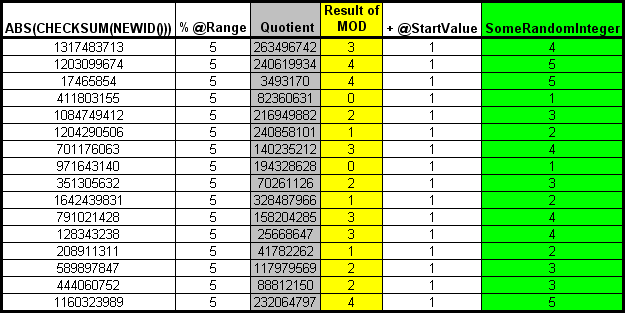
The MODULO 5 works on large numbers just like it does the small ones.  Looking at the Integer Remainder column, we've successfully limited the random numbers returned to 5 unique numbers from 0 to 4. All that remains to get the random values of 1 to 5 is to add the starting value of "1" to the Remainder.

Making the substitutions for @Range and @StartValue for our 1 thru 5 problem, the random integer formula would boil down to the following.

SomeRandomInteger = ABS(CHECKSUM(NEWID())) % 5 + 1

Putting it in terms of the random integer formula, here's what we get. The answer to the entire formula is in the Green column.

For random integers from 400 to 500 and using the same random values, the random integer formula would boil down to this.

SomeRandomInteger = ABS(CHECKSUM(NEWID())) % 101 + 400

The chart would look like this.

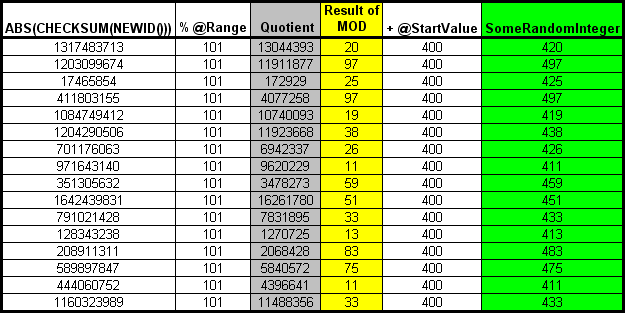
Notice that, in this case, the minimum value of 400 and the maximum value of 500 were not included. That's because the values of 400 thru 500 is nothing but it limit. The random numbers returned could be anything within those limits and, as with any random number, the numbers can repeat themselves before all possible values of the limits have been exhausted.

* - Simple Multiplication – Applying the "Limit" for Random Floats

In code, applying limits for random floats looks nearly identical to applying limits to random integers. Under the covers, it's a whole lot different, though. Here's the formula for generating random floats.

SomeRandomFloat = RAND(CHECKSUM(NEWID())) * @Range + @StartValue

As previously discussed, the part of that formula that generates random floats is RAND(CHECKSUM(NEWID()))and it generates float values from 0 up to and NOT including 1. To be specific, it can generate values from 0 to 0.99999999999999. If we want to generate random floats from 1 to 5, the value of @Range is still, 5 because we subtract 1 from 5 and add 1 back in. Here's what a chart of 16 random floats multiplied by a RANGE of 5 would look like.

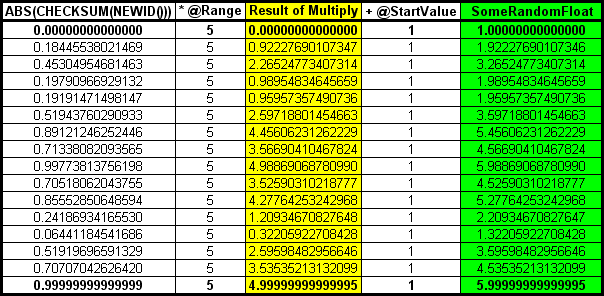
I've included the min and max limits of what RAND() can return to show you how the limits work for the 1 thru 5 problem. The rest of the rows are in a random order but still between the min and max limits of RAND().

The first row shows the min limit of RAND() as being 0. Multiplying the 0 times our RANGE value results in 0 (in the Yellow column). Adding our starting value of 1 returns the "1" (Green column) of our 1 thru 5 problem.

The last row shows the max limit of RAND() as being "not quite 1" or 0.99999999999999. When we multiply that number times our RANGE value, we end up with a number very close to 5 but we're not done yet. The formula will still add the starting value and we end up with a maximum random float for our 1 thru 5 problem of almost 6 which is well above the value of 5! You might, at first, consider that to be a fault but don't. The code still works as advertised. It's capable of returning any and all floats that start with 1 thru 5.

Calculating a range of random floats from 400 to 500 using the same random numbers would end up looking like this.

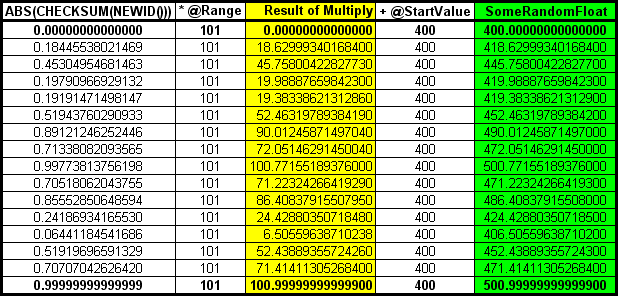
Adjusting the Range to be "Non-Inclusive"

If what you really want to do is generate all values from 1 up to and NOT including 5, then simply don't add the +1 in the calculation of the RANGE value. In other words, calculate the RANGE as @EndValue - @Startvalue without adding an extra "1". Like this…

--===== The "Non-Inclusive Range" Formula
 SELECT @Range = @EndValue - @StartValue

As you'll see in Part 2 of this series, this particular RANGE formula has many uses that will make your life a whole lot easier when calculating randomized floats including when you're calculating dates with times and 2 decimal place currency amounts (for example).

Using the same random floats as we used before, here are the results of the 1 to 5 problem using the "Non-Inclusive Range" formula. Notice the values returned are from 1 to "something less than 5".

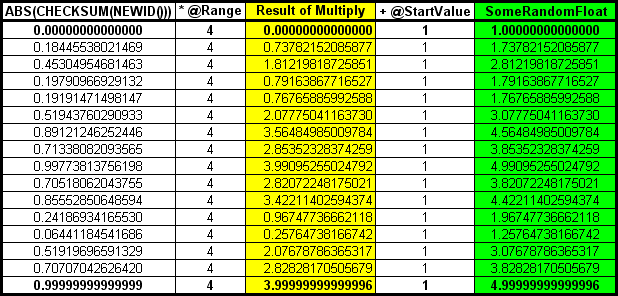
Summary

The generation of test data doesn't need to be a time consuming or difficult chore. Using tools such as a TOP limited Cross Join and SELECT/INTO, we can build a million rows of data in scant seconds with very little coding effort. Through the use of some standard functions and some simple math, we can easily control the domain of numbers that our random integer and float generation code returns.

In Part 2 of this series, we'll learn how to create all sorts of different test data using those simple random numbers.

Thanks for listening, folks.

--Jeff Moden

© Copyright 2012, Jeff Moden, All Rights Reserved.

¹ RBAR is pronounced "ree-bar" and is a "Modenism" for "Row-By-Agonizing-Row".