What are the odds of ...
In this post am attempting to explore what can be deemed to be the most commonly used statistical concept - the odds ratio. We use this all the time when we examine what are the odds of this against that. We use it to feel better about certain habits, to predict outcomes of various situations, to win a bet and so on.
The terms probability and odds ratio are not quite the same, although they are often used as synonyms. The differences are well illustrated in this article, for those interested. Simply put, odds are expressed as ratios while probability is expressed as a fraction or a percentage of an outcome.
What is an odds ratio? Given a situation, what are the chances of an outcome, versus another outcome. What are the chances of this person winning the election versus that person, given that we have just the two of them as candidates? In an ideal world, not knowing or considering any other factors, the odds ratio should be 1:1 or a 50% percent chance.
Odds ratios are used extensively in calculating illness versus exposure. Let us take a very common example. What are the odds of heavy smokers facing early illness/death versus non smokers? To calculate this we need 4 numbers from a sample of people we are using to study :
| Sick | Healthy | Total | |
| Smoking | n11 | n10 | n11+n10 |
| Non smoking | n01 | n00 | n01+n00 |
Odds of sickness for smoking = (n11/n11+n10)/(n10/n11+n10) = n11/n10
Odds of sickness for non smoking = (n01/n01+n00)/(n00/n01+n00) = n01/n00
So, odds of sickness for smoking compared to non smoking would be
(n11/n10)/(n01/n00)..
An odds ratio of one indicates that the chances are the same for getting sick for someone who is a smoker as well as someone who is a non smoker. An odds ratio of > 1 indicates a smoker has higher chances, and a odds ratio of < 1 indicates that smoker has lower chances.
Now, R has no built in functions for such a simple math calculation, and this can be easily done with TSQL as well. But after this comes the hard part. The odds ratio in itself is not enough to predict odds of a situation. We need a 'confidence interval' to go with it. In other words, we need to be able to say how confident we are that this data sample we are using reflects the real world accurately? Ideally, a 95% confidence level is considered good enough to draw relevant conclusions.
We have to be able to say that 95% of the time the correlation between smoking status and health is in the range of x and y, where x and y are considered upper and lower confidence intervals. The formula to calculate upper and lower confidence intervals is something like this:
Lower confidence interval = Log(OR) - 1.96* Standard Error* LN(OR)
Upper confidence interval = Log(OR) + 1.96* Standard Error* LN(OR)
Standard Error = sqrt(1/n00+1/n01+1/n10+1/n11)
I created some data on my own to demonstrate how this works. The scripts for data can be found here.
Below is the T-SQL script I wrote to calculate odds ratio from data,
DECLARE @n00 decimal(8, 2), @n11 decimal(8, 2), @n10 decimal(8, 2), @n01 decimal(8, 2)
DECLARE @or decimal(8, 2)
SELECT @n00 = sum(numberofpeople)
FROM [WorldHealth].[dbo].[smokers]
WHERE Smokingstatus = 0 and healthyorsick = 0;
SELECT @n01 = sum(numberofpeople)
FROM [WorldHealth].[dbo].[smokers]
WHERE Smokingstatus = 0 and healthyorsick = 1;
SELECT @n10 = sum(numberofpeople)
FROM [WorldHealth].[dbo].[smokers]
WHERE Smokingstatus = 1 and healthyorsick = 0;
SELECT @n11 = sum(numberofpeople)
FROM [WorldHealth].[dbo].[smokers]
WHERE Smokingstatus = 1 and healthyorsick = 1;
SELECT @N11/@N10,@N00/@N01
SELECT @or = (@n11/@n10)*(@n00/@n01);
SELECT 'Odds of getting sick early for smokers versus non smokers:' as 'ODDS', @or as OddsRatio;
--SELECT sqrt((1/@n00) + (1/@n01) + (1/@n10) + (1/@n11))
SELECT
exp(LOG(@or) - (1.96*sqrt((1/@n00) + (1/@n01) + (1/@n10) + (1/@n11)))) as lowconfidenceinterval,
exp(LOG(@or) + (1.96*sqrt((1/@n00) + (1/@n01) + (1/@n10) + (1/@n11)))) as highconfidenceinterval
The result I got from running this script in Management Studio is shown below:
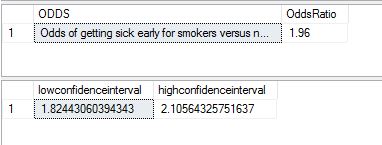
Next, I tried using R code to achieve the same results. Below is the script i used for R (run within Microsoft's R Studio:
#Install and load packages for R
install.packages("RODBC")
library(RODBC)
#set up connection to the database
cn <- odbcDriverConnect(connection="Driver={SQL Server Native Client 11.0};server=MALATH-PC\\SQL01;database=WorldHealth;Uid=sa;Pwd=<mypwd>")
#Getting data to calculate odds ratio
n00 <- sqlQuery(cn, 'SELECT sum(numberofpeople) FROM [WorldHealth].[dbo].[smokers] WHERE Smokingstatus = 0 and healthyorsick = 0',believeNRows = FALSE)
n01 <- sqlQuery(cn, 'SELECT sum(numberofpeople) FROM [WorldHealth].[dbo].[smokers] WHERE Smokingstatus = 0 and healthyorsick = 1',believeNRows = FALSE)
n11 <- sqlQuery(cn, 'SELECT sum(numberofpeople) FROM [WorldHealth].[dbo].[smokers] WHERE Smokingstatus = 1 and healthyorsick = 1',believeNRows = FALSE)
n10 <- sqlQuery(cn, 'SELECT sum(numberofpeople) FROM [WorldHealth].[dbo].[smokers] WHERE Smokingstatus = 1 and healthyorsick = 0',believeNRows = FALSE)
OR<-(n11/n10)*(n00/n01)
#Calculating upper and lower confidence levels
logor<-log(OR)
loglo<-logor-1.96*siglog
loghi<-logor+1.96*siglog
ORlo<-exp(loglo)
ORhi<-exp(loghi)
cat("Lower confidence interval",unlist(ORlo))
cat("Odds Ratio",unlist(OR))
cat("Higher Confidence Interval",unlist(ORhi))
Below are my results from running the code within R Studio.
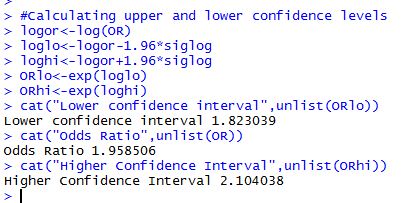
I can see from both cases that I have an Odds Ratio of about 1.96 times smokers getting sick versus non smokers. I can say with 95 percent confidence that this is likely to vary between a low 1.82 to a high 2.10 for the selected sample.
It is possible to run the R script from within SQL Server, but in this particular case that does not serve any real purpose as we are not using any of R's built in functions that give us an advantage over T-SQL. This is just an example of how we can get results using T-SQL or R, either works simply and well
For more advanced statistical calculations we may lean towards R as the preferred method. Hope to write more on that going forward. Thank you for reading.




