No, no, no. The song has nothing to do with this article. It’s not about war, it’s about the Banker’s Rounding method, so we don’t pull the second part of the quote in here. The method is widely used, so it must be good for something. In this article I’m trying to find out what for exactly.

Genesis

For the beginning let’s see with which problem this method is called on to solve. For this purpose, I’ve created a simple test set of randomly selected decimal numbers with 4 decimal places:

-- drop table #RandomN
DECLARE @TotalSet int 
set @TotalSet = 10000000
IF OBJECT_ID ('tempdb..#RandomN') IS NULL
select CONVERT(decimal( 10,4), CONVERT(FLOAT, convert(int, CRYPT_GEN_RANDOM(3)))/10000) N 
INTO #RandomN
from service.dbo.TallyGenerator (1, @TotalSet, NULL, 1)

dbo.TallyGenerator is a function creating a set of sequential numbers within the range defined by its parameters. You may find the script for it here: https://www.sqlservercentral.com/scripts/tally-generator

The bigger the number of @TotalSet, the more even distribution we’re gonna get and more reliable results we may expect.

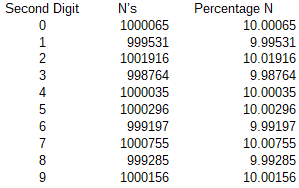
I’m planning to perform standard “to cents” rounding. Before doing that I want to see how 2^nd digits after the decimal point are distributed across the range:

select SecondDigit, count(n), 
count(n)*convert(float, 100) / @TotalSet Percentage
FROM (
select floor( n*100%10) SecondDigit, n
from #RandomN T1
) T2
group by SecondDigit
order by SecondDigit

The output:

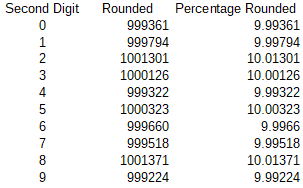
Now, let’s see how it changes after we round the numbers to that 2^nd digit we’ve just inspected. It is pretty even, as the level of deviation matches the statistical expectation.

select count(Rounded), 
RoundedSecondDigit, count(Rounded)*convert(float, 100) / @TotalSet PercentageRounded
FROM (
select floor( round(n, 2)*100%10) RoundedSecondDigit
, round(n, 2) Rounded, n
from #RandomN T1
) T2
group by RoundedSecondDigit
order by RoundedSecondDigit

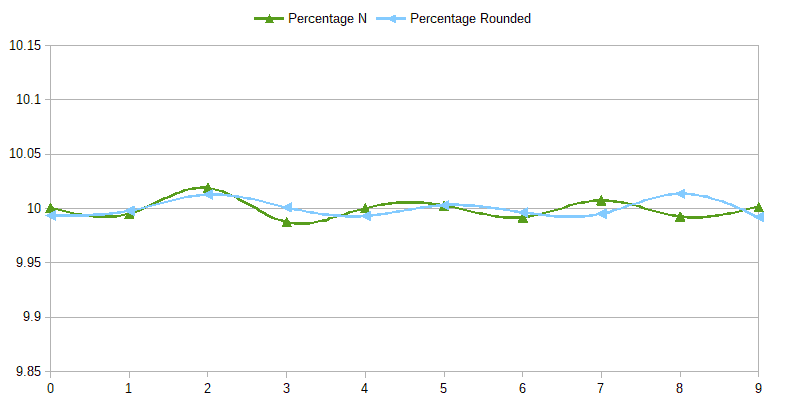
I visualized the result set with the following graph:

This looks pretty good. The distribution is pretty even, the one of the rounded numbers does not exactly follow the original one, but it’s not supposed to.

The Issue

So, what’s the problem? Those who used the Banker’s Rounding must already know the answer. The problem is here:

SELECT SUM(n) TotalOriginal, SUM(round(n,2)) TotalRounded
FROM #RandomN T1

The output of this query on the current dataset in #Random returned this:

On your set the numbers may be slightly different, but regardless of the actual numbers in your random test the pattern will be the same: the 8^th digit from the left will be increased by 5 ± random variation, depending on the size of your test set.

The source of the issue is pretty easy to see. In the half-open interval between two whole numbers, say 0 and 1, we have 100 “cents”, which we have to round. Half of them are rounded up, half of them down. Rounding each of this numbers adds some imprecision to to the final total.

• 0.07 is rounded to 0.00 – adds -0.07;
• 0.58 is rounded to 1.00 – adds +0.42.

All those numbers may be grouped in pairs compensating for each other’s deviation:

0.01 <--> 0.99;

0.02 <--> 0.98;

....

0.48 <--> 0.52

0.49 <--> 0.51.

The imprecision created by each of those pairs is exactly 0.00, so the total deviation made up by all of them would be also 0.00.

Only 2 numbers are left out of the pairing: 0.00 and 0.50 – first one does not create any deviation, and the second one adds +0.50: that’s exactly the “5” in the 8^th position of our 10 million numbers total.

Is it actually an issue?

Well, any good mathematician (or other scientist) would say that such a deviation in rounded total should not be considered as a problem, for two reasons:

First, as soon as we start rounding we stepped into the realm of “imprecise” computing, and the rules of imprecise math should apply here. If we add up 2 numbers having 3 significant digits then the result has a precision of ±0.5 of the last digit. 4^th digit cannot be trusted and must not be taken into account.

For example, if we add previously rounded numbers 755 and 545 then the result cannot be recorded as 1300, as it would be indicate the 4^th significant digit. The correct result would be 130*10, or in true scientific notation, 1.30E3. I left the first zero in place, because it’s a truly significant digit and, unlike the following zero,  may/must be taken into account in following calculations.

According to this approach, we can keep only 7 first digits in our rounded total (well, 6 to be pedantic, but considering the randomness of the source numbers we may allow 7^th digit to stay) and must discard the rest of them.

Second, we adding up the numbers from the open interval: from 0.00 incl. to 1.00 excl. The smallest number we round is 0.00, and the biggest number is 0.99. Which puts the middle of the interval not actually into the middle, but closer to the right side of it.

All the exact numbers we have in this interval add up to 49.5, when anyone who’s been studying math in school knows that Integral of the function (y=x/100) on the interval [0;100) equals 50. It happens because an exact number of say, 0.33, actually represents all the possible rational numbers with values between 0.33 incl. and 0.34 excl. For example, 1/3, or 121/365. Those rational numbers are natural products of various banking calculations, e.g. distributed payments, shared liabilities, rates applied, etc.

Therefore it’s the original, exact, number representation which is at fault, due to skewing the overall totals down by 0.5, and the rounding actually fixes that error.

Still an issue – pending resolution

OK, the argument may look strong, but there is one issue with it. The Big Daddy from the Bank most likely won’t be willing even to listen to this “academic nonsense”:

“- The numbers must add up! Make it happen! Now! If cannot do it I’ll find somebody else who’ll do it!”

And you know what? It must be not that hard to find someone who’ll happily exchange the principles of mathematical correctness for an appreciation from the Big Daddy. Especially when that appreciation is reflected in positive changes on personal bank account, no matter how correctly rounded.

So, the solution is simple: if rounding of halves up adds an extra 0.5 to the total, then lets round half of the halves up and another half of the halves down. This way they’ll compensate for each other and bring the totals to the state requested by the Boss.

OK, let’s do it.

The Bankers Rounding function is borrowed from Lynn Pettis, posted originally here: https://www.sqlservercentral.com/forums/topic/bankers-rounding-in-t-sql-like-math-round-in-net/page/3

May be it's not the best implementation in terms of performance or other criteria (or may be it is, the name on it is pretty credible, still - I did not bother to check), but it seems producing correct results according to Banking Rounding definitions, and it's the only thing which matters to me for the purpose of this article.

So, how did we do?

Let’s start with the totals:

SELECT SUM(n) TotalOriginal, SUM(round(n,2)) TotalRounded, SUM([dbo].[fn_BRound](n, 2) ) TotalBankersRounded
FROM #RandomN T1

That’s way better. Not exact match, but we cannot expect it from a random data set.

Now let’s see how did we do with the digit distribution:

select count(BankerRounded), 
BankerRoundedSecondDigit, count(BankerRounded)*convert(float, 100) / @TotalSet PercentageBankerRounded
FROM (
select floor([dbo].[fn_BRound](n, 2)*100%10) BankerRoundedSecondDigit
, [dbo].[fn_BRound](n, 2) BankerRounded, n
from #RandomN T1
) T2
group by BankerRoundedSecondDigit
order by BankerRoundedSecondDigit

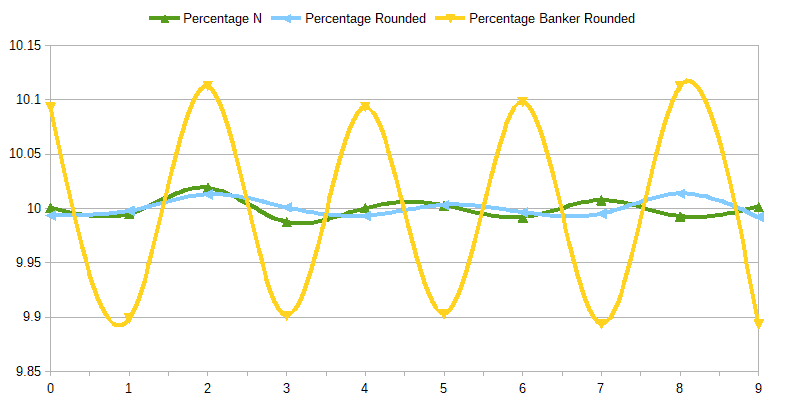
After adding the result set returned by this query to the previously posted graph it becomes this:

Oops. It cannot be right. The original, pretty even, distribution of the target digits is significantly distorted by the Banking rounding. Now the presence of the even numbers in the last significant digits in the resulting data set is increased by about 1%, at the expense of the odd ones, whose presence is decreased by the same rate.

That could only mean that certain numbers in the resulting data set are made deliberately less precise, for the sake of making the total amount look better.

These observations bring us to the ...

Conclusions

1. Rounding of decimal numbers inevitably presents a systemic error caused by imprecise representation of vast majority of rational numbers (which are inexact by nature) with exact decimal formats.

2. Banking rounding is called to bring totals of rounded numbers to totals of original decimal numbers by deliberately distorting some of the rounded values.

This method of rounding alters the result by modifying insignificant numbers, which must be, according to the mathematical rules, ignored after the rounding, as they are beyond of precision of each summarised rounded number.

3. Any conversion of rational values to decimal format inevitably causes some form of rounding. Each rounding decreases the precision of the outcome. To maintain the best precision of the final result all intermediate calculations must be performed on numbers in floating point formats, and the rounding must be performed (if necessary) only on the final data set.