Introduction
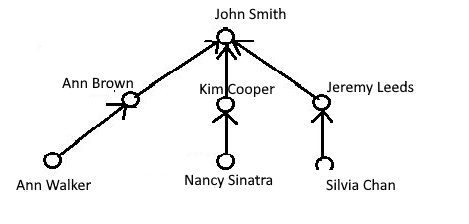
Employee lists in organizations are often maintained in spreadsheets or database tables which record each employee’s number, name, position and so on. As well, each employee has a Position Number and Parent Position (or something like that) so the manager of each employee can be located:
Position Parent Employee Position First Name Last Name Employee Email Location Number Position Number 12345 12345 91919 President & CEO John Smith John.Smith@Hospital.com ABC 683 23456 12345 23456 Director Office Of President Ann Brown Ann.Brown@Hospital.com ABC 683 34567 12345 34567 Chief Financial Officer Kim Cooper Kim.Cooper@Hospital.com ABC 683 45678 12345 45678 Executive Director Jeremy Leeds Jeremy.Leeds@Hospital.com ABC 683 56789 23456 56789 Manager Financial Analysis Ann Walker Ann.Walker@Hospital.com CRH 989 67890 34567 67890 Financial Analyst Nancy Sinatra Nancy.Sinatra@Hospital.com CRH 244 91234 45678 78901 Financial Analyst Silvia Chan Silvia.Chan@Hospital.com ABE 123 92345 56789 89012 Financial Analyst Jane Begg Jane.Begg@Hospital.com ABC 683 93456 67890 90123 Financial Analyst Lan Wang Lan.Wang@Hospital.com ABC 683
But listing those employees who work under a given manager (directly or indirectly) is difficult to accomplish with such tables. Even more difficult would be queries like “Show me the ratio of employees to direct reports for managers four steps below the CEO”.
This article shows how to ask such questions on those tables by simply viewing them as trees. Furthermore, the stored procedure provided here to ask those questions works for any hierarchical table (those that have a “parent-of” relationship between records) such as security or budgeting tables. No changes to the table are needed because a temporary copy is used for any queries submitted to it. It also allows one to add four useful columns to the source table so that complex questions like the one above may be queried directly to it with simple SQL. This procedure can also be used to update those columns in the source table whenever records are modified.
This is the first of two articles showing how topological sorting [1] can be used by database programmers. The algorithm presented here is based on an earlier article [2] for preserving referential integrity in ETL migrations (which will be generalized for directed graphs in the second article). The resource section contains a print-ready copy of this article in PDF format along with the listing of the stored procedure.
What Is A Tree?
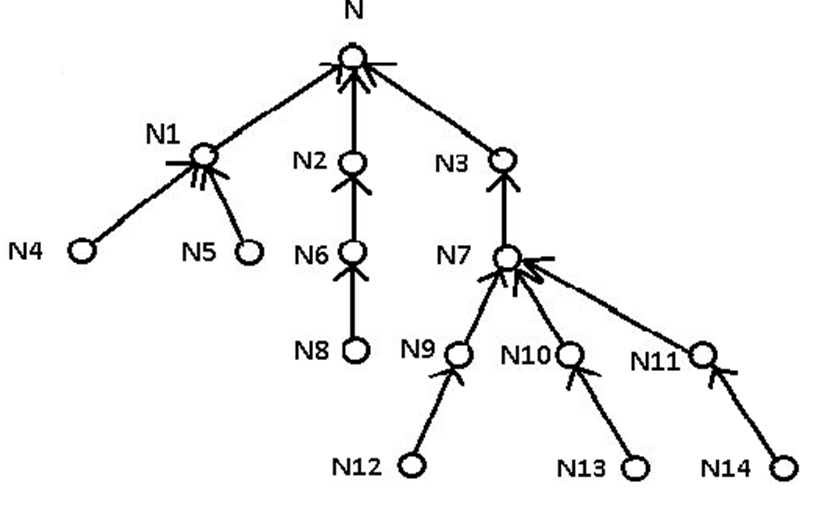
Strictly speaking, a tree is any undirected graph where a unique path exists between any two nodes (or vertices). By arbitrarily selecting any node as its top node, the remaining nodes each inherit a unique path to the top node, which gives each edge a natural direction. That’s because each node can “point to” the unique node that begins its path to the top node. But it’s common to build trees in the opposite direction by explicitly using a parent_of relationship as shown above (parent_of = Parent Position) where it defines directed edges between the nodes that lead them up to the top node:
The top node is always the unique record whose parent is NULL. Those nodes with no edges leading to them are called leaves. In the above tree N4, N5, N8, N12, N13, N14 are its leaves. The predecessors of any node are those nodes on its unique path to the top node. For example, the predecessors of N7 are N3, N. The descendants of any node are those nodes on any path from the leaves to it. For example, the descendants of N7 are N9, N10, N11, N12, N13, N14.
Here is another image, using the sample data at the top of the article for a partial view of the tree.
Several issues may occur with this approach, all of which need to be fixed before any queries can be reliably executed:
- There may be zero (or more than one) record whose parent is NULL
- The parent_of value in one record may refer to another record in the table that doesn’t exist (orphan)
- The parent_of values may create a loop among the records (eg. A -> B -> C -> A)
This procedure will check these issues and list the errant nodes in any loop so they can be fixed. For example, in the above spreadsheet the first record is declared to be its own parent, so it represents a loop from a node to itself.
Four attributes of nodes are computed by the proc to help build complex queries on trees:
| numDescendants | Number of descendants of a node |
| numChildren | Number of nodes directly below a node |
| Height | Length of longest path from a node to its leaves |
| Depth | Length of path from a node to the top node |
For example, for the node N7 in the above tree:
- The number of descendants = 6
- The number of children = 3
- Height = 2
- Depth = 2
Using The Procedure
The tree verification procedure needs to know the names of the key, name and parent_of columns of the source table, which will be renamed NodeId, Node, ParentId in the temporary table. To do this, the procedure dbo.sp_VerifyTree accepts the following parameters:
| @Schema | Schema of table containing tree |
| @Graph | Table containing tree |
| @NodeId | Column name for NodeId in table containing tree |
| @Node | Column name for Node in table containing tree |
| @ParentId | Column name for ParentId in table containing tree |
| @DDL | DDL code to execute first (optional) |
| @DML | DML code to execute last (optional) |
For example, in the above spreadsheet:
- @NodeId = ‘Position Number’
- @Node = ‘Employee Email’
- @ParentId = ‘Parent Position’
The @DDL and @DML parameters accept any SQL statement.
The idea is that if you want to run, for example, queries on newly created columns, then create them with the @DDL parameter before executing the queries with the @DML parameter. For that reason, the @DDL code is executed first by the procedure.
How The Procedure Works
The procedure first copies the @NodeId, @Node, @ParentId columns of the original table into a temporary table ##Tree before verifying it's a tree. It does this by attempting to perform a topological sort of its nodes. That is, it attempts to sort the nodes by the length of their longest paths to their leaves. It does this by first selecting all the nodes with no children (so the lengths of their longest paths = 0) then removing them and their edges before starting over with what’s left of the tree. Of course, the lengths of the longest paths for the leaves in the remaining tree must be incremented, for the original tree, by the current number of passes each time this happens. It continues this way until no more nodes are left. Assuming no loops exist in the table, this process will take no more steps than the number of nodes because it will remove at least one node on each pass. If it takes more steps than that, then the proc halts because it knows that the remaining edges must form a series of loops, which is the only way their nodes can indefinitely avoid removal.
If the attempt is successful, if adds four useful columns to ##Tree that are available to any SQL statement passed to the @DDL and @DML parameters:
- NumDescendants
- NumChildren
- Depth
- Height
It then populates them by using a simple loop to update NumDescendants; NumChildren after initializing both to 0.
The code is shown here:
-- Crawl up the tree from its leaves
-- Note that this computation for nodes at each height employs the values of its children
-- That is why an UPDATE is executed at each level, working upward from its leaves (Height = 0)
SET @I = 0
WHILE @I < @NumNodes
BEGIN
SET @I = @I + 1
UPDATE g
SET
g.NumDescendants = (SELECT sum(NumDescendants) FROM ##Tree h where h.Parentid = g.Nodeid) +
(SELECT count(*) FROM ##Tree k where k.Parentid = g.Nodeid),
g.NumChildren = (SELECT count(*) FROM ##Tree i where i.Parentid = g.Nodeid)
FROM ##Tree g
WHERE g.NodeId IN (SELECT Nodeid FROM #Height WHERE Height = @I)
END
and a common table expression to update Depth:
-- Crawl down the tree from its top node
IF OBJECT_ID(N'tempdb..#Depth') IS NOT NULL DROP TABLE #Depth
;WITH cte (NodeId, Depth) AS (
SELECT NodeId, 0 AS Depth -- Add top node to cte
FROM ##Tree
WHERE NodeId = (SELECT TOP 1 NodeId WHERE ParentId IS NULL)
UNION ALL
SELECT g.NodeId, cte.Depth + 1 AS Depth -- Add children of nodes currently in cte
FROM ##Tree g
INNER JOIN cte ON cte.NodeId = g.ParentId
)
SELECT NodeId, Depth INTO #Depth FROM cte -- Collect all depths from cte into #Depth
UPDATE g
SET g.Depth = h.Depth
FROM
##Tree g INNER JOIN #Depth h
ON g.NodeId = h.NodeId
The creation of #Height occurs when the proc attempts to perform a topological sort, after which Height may be updated from it:
-- Update Height UPDATE t SET t.Height = h.Height FROM ##Tree t INNER JOIN #Height h ON t.NodeId = h.NodeId.
Sample Data
To run the samples below, we will set up the table and data. This is the sample data for the tree shown in the image above.
IF EXISTS (SELECT * FROM sys.objects WHERE object_id = OBJECT_ID(N'[dbo].[Graph]') AND type in (N'U'))
DROP TABLE [dbo].[Graph]
GO
CREATE TABLE [dbo].[Graph](
[NodeId] [int] IDENTITY(0,1) NOT NULL,
[Node] [varchar](128) NOT NULL,
[ParentId] [int] NULL
) ON [PRIMARY]
GO
SET NOCOUNT ON
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N',NULL)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N1',0)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N2',0)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N3',0)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N4',1)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N5',1)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N6',2)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N7',3)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N8',6)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N9',7)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N10',7)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N11',7)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N12',9)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N13',10)
INSERT INTO dbo.[Graph](Node,ParentId) VALUES('N14',11)
The code for the procedure is at the bottom of this article.
Now, let's see some sample runs.
Sample Run 1
If the above tree exists in the table dbo.Graph where it already has the correct column names NodeId, Node, ParentId (so they don’t need to be re-named by the procedure), then the following invocation will attempt to verify it’s a tree and return @ERROR_NUMBER = 0.
DECLARE @ERROR_NUMBER INT DECLARE @ERROR_MESSAGE VARCHAR(MAX) DECLARE @ROW_COUNT INT EXEC @ERROR_NUMBER = dbo.sp_VerifyTree @Schema = 'dbo', -- schema of table containing tree @Graph = 'Graph', -- table containing tree @NodeId = 'NodeId', -- column name for NodeId in table containing tree @Node = 'Node', -- column name for Node in table containing tree @ParentId = 'ParentId', -- column name for ParentId in table containing tree @DDL = '', -- DDL code to execute first (optional) @DML = '', -- DML code to execute last (optional) @ERROR_NUMBER = @ERROR_NUMBER OUTPUT, @ERROR_MESSAGE = @ERROR_MESSAGE OUTPUT, @ROW_COUNT = @ROW_COUNT OUTPUT SELECT @ERROR_NUMBER AS ERROR_NUMBER, @ERROR_MESSAGE AS ERROR_MESSAGE, @ROW_COUNT AS ROW_COUNT
The results of this run are shown here. We can see that there error_number is returned as 0, so this is a tree with 15 nodes.

Sample Run 2
The following invocation stores #Height and #Depth in temporary tables that are available after the procedure ends.
DECLARE @ERROR_NUMBER INT DECLARE @ERROR_MESSAGE VARCHAR(MAX) DECLARE @ROW_COUNT INT EXEC @ERROR_NUMBER = dbo.sp_VerifyTree @Schema = 'dbo', -- schema of table containing tree @Graph = 'Graph', -- table containing tree @NodeId = 'NodeId', -- column name for NodeId in table containing tree @Node = 'Node', -- column name for Node in table containing tree @ParentId = 'ParentId', -- column name for ParentId in table containing tree @DDL = ' IF OBJECT_ID(N''tempdb..##MyHeight'') IS NOT NULL DROP TABLE ##MyHeight; IF OBJECT_ID(N''tempdb..##MyDepth'') IS NOT NULL DROP TABLE ##MyDepth; ', -- DDL code to execute first (optional) @DML = ' SELECT * INTO ##MyHeight FROM #Height; SELECT * INTO ##MyDepth FROM #Depth; ', -- DML code to execute last (optional) @ERROR_NUMBER = @ERROR_NUMBER OUTPUT, @ERROR_MESSAGE = @ERROR_MESSAGE OUTPUT, @ROW_COUNT = @ROW_COUNT OUTPUT SELECT @ERROR_NUMBER AS ERROR_NUMBER, @ERROR_MESSAGE AS ERROR_MESSAGE, @ROW_COUNT AS ROW_COUNT SELECT NodeId, Height FROM ##MyHeight SELECT NodeId, Depth FROM ##MyDepth
When this code runs, we again get the same results as the first 1 in a result set. We then get two other result sets. The first one shows the node height and looks this:
NodeId Height 4 0 5 0 8 0 12 0 13 0 14 0 1 1 6 1 9 1 10 1 11 1 2 2 7 2 3 3 0 4
Those nodes at the bottom, or leaf level, have a height of 0. Those that have only one level below them show a height of 1, those with 2 levels of nodes show 2, and so on. Node 4 is at the bottom, and has a height of 0. Node 1 has N4 and N5 below it at one level, so a height of 1. Node 7 has two levels of nodes below it. The top node has a height of 4.
The last result set shows the depth. The results are here, with the depth being the distance from the top node. These are the inverse of the height numbers above.
NodeId Depth 0 0 1 1 2 1 3 1 7 2 9 3 10 3 11 3 14 4 13 4 12 4 6 2 8 3 4 2 5 2
Sample Run 3
The following invocation adds the columns numDescendants, numChildren, Height, Depth to the original table and updates them from the temporary table. To do this repeatedly, set @DDL = ‘’ after the first run.
DECLARE @ERROR_NUMBER INT DECLARE @ERROR_MESSAGE VARCHAR(MAX) DECLARE @ROW_COUNT INT EXEC @ERROR_NUMBER = dbo.sp_VerifyTree @Schema = 'dbo', -- schema of table containing tree @Graph = 'Graph', -- table containing tree @NodeId = 'NodeId', -- column name for NodeId in table containing tree @Node = 'Node', -- column name for Node in table containing tree @ParentId = 'ParentId', -- column name for ParentId in table containing tree @DDL = ' -- Add columns to source table ALTER TABLE dbo.Graph ADD numDescendants int NULL; ALTER TABLE dbo.Graph ADD numChildren int NULL; ALTER TABLE dbo.Graph ADD Height int NULL; ALTER TABLE dbo.Graph ADD Depth int NULL; ', -- DDL code to execute first (optional) @DML = ' -- Update columns in source table UPDATE g SET g.NumDescendants = t.NumDescendants, g.NumChildren = t.NumChildren, g.Height = t.Height, g.Depth = t.Depth FROM dbo.Graph g INNER JOIN ##Tree t ON g.NodeId = t.NodeId SELECT * FROM dbo.Graph ', -- DML code to execute last (optional) @ERROR_NUMBER = @ERROR_NUMBER OUTPUT, @ERROR_MESSAGE = @ERROR_MESSAGE OUTPUT, @ROW_COUNT = @ROW_COUNT OUTPUT SELECT @ERROR_NUMBER AS ERROR_NUMBER, @ERROR_MESSAGE AS ERROR_MESSAGE, @ROW_COUNT AS ROW_COUNT
The results here are two sets. The second is the error set, which shows 0. The first one describes the tree:
NodeId Node ParentId numDescendants numChildren Height Depth 0 N NULL 14 3 4 0 1 N1 0 2 2 1 1 2 N2 0 2 1 2 1 3 N3 0 7 1 3 1 4 N4 1 0 0 0 2 5 N5 1 0 0 0 2 6 N6 2 1 1 1 2 7 N7 3 6 3 2 2 8 N8 6 0 0 0 3 9 N9 7 1 1 1 3 10 N10 7 1 1 1 3 11 N11 7 1 1 1 3 12 N12 9 0 0 0 4 13 N13 10 0 0 0 4 14 N14 11 0 0 0 4
Now we can go directly to the source table and use simple SQL to show the ratio of employees to direct reports for managers one step below the CEO:
SELECT *, numDescendants/numChildren AS 'numDescendants/numChildren ' FROM dbo.Graph WHERE numChildren > 0 AND Depth = 1 ORDER BY numDescendants/numChildren DESC
The results of this are:
| NodeId | Node | ParentId | numDescendants | numChildren | Height | Depth | numDescendants/numChildren |
| 3 | N3 | 0 | 7 | 1 | 3 | 1 | 7 |
| 2 | N2 | 0 | 2 | 1 | 2 | 1 | 2 |
| 1 | N1 | 0 | 2 | 2 | 1 | 1 | 1 |
Summary
This article shows code and a method for describing a set of data as a tree and how you can analyze the relationships with the data in the table.
Procedure Code
Here is the listing For sp_VerifyTree:
CREATE PROCEDURE [dbo].[sp_VerifyTree]
(
@Schema VARCHAR(128) -- Schema of table containing tree
,@Graph VARCHAR(128) -- Table containing tree
,@NodeId VARCHAR(128) -- Column name for NodeId in table containing tree
,@Node VARCHAR(128) -- Column name for Node in table containing tree
,@ParentId VARCHAR(128) -- Column name for ParentId in table containing tree
,@DDL NVARCHAR(MAX) = '' -- DDL code to execute after successful test (optional)
,@DML NVARCHAR(MAX) = '' -- DML code to execute after successful test (optional)
,@ERROR_NUMBER INT OUTPUT -- Return error number
,@ERROR_MESSAGE VARCHAR(MAX) OUTPUT -- Return error message
,@ROW_COUNT INT OUTPUT -- Return number of rows affected (-1 = not set)
) AS
BEGIN
/*
Script: Verify that the table @Graph represents a tree and (optionally) execute custom SQL.
Notes: This proc copies the columns @NodeId, @Node, @ParentId in the table @Graph
to a temporary table ##Tree which has the column names NodeId, Node, ParentId
used by it. It then determines if the temporary table represents a tree. Additionally,
custom SQL may be executed on either table after a successful test.
The source table @Graph must have a column referencing the "parent" record of any record.
The name @ParentId of that column is changed to ParentId in the temporary table, along
with changes to @NodeId (key of mode) and @Node (name of node).
@NodeId must convert to INT.
An undirected graph is called a tree when every two nodes have exactly one
undirected path connecting them. If this proc concludes that the table doesn't
represent a tree, the errant nodes are listed to show why.
It does this by attempting to topologically sort the tree, checking for loops in the
directed edges defined by the ParentId relationship which would imply that it wasn't a tree.
Specifically, it checks that:
1) Exactly one node has a NULL ParentId
2) No looping occurs with the ParentId relationship (eg. A -> B -> ... -> A)
It is easy to prove that the above conditions imply that the nodes and undirected edges
of @Graph represent a tree.
*/-- Declarations
DECLARE @SQL NVARCHAR(MAX)
DECLARE @Height INT
DECLARE @FakeNodeId INT
DECLARE @NumNodes INT
DECLARE @COUNT INT
DECLARE @I INT
DECLARE @is_nullable BIT
-- No counting
SET NOCOUNT ON
-- Assume that @ROW_COUNT is not being computed
SET @ROW_COUNT = -1
-- To compute @ROW_COUNT anywhere for debugging purposes, enter
-- SET @ROW_COUNT = @@ROWCOUNT
-- immediately after any SELECT, INSERT, DELETE or UPDATE statement
-- and the last value it computes will be returned
BEGIN TRY
/*
Set up and populate ##Tree
*/-- Drop, re-create and populate global temporary table ##Tree with @NodeId, @Node, @ParentId from @Graph
IF OBJECT_ID(N'tempdb..##Tree') IS NOT NULL DROP TABLE ##Tree
SET @SQL = 'SELECT [' + @NodeId + '] AS NodeId, [' + @Node + '] AS Node, [' + @ParentId + '] AS ParentId INTO ##Tree FROM [' + @Schema + '].[' +@Graph +']'
EXEC dbo.sp_executeSQL @SQL
-- Determine the number of nodes in the tree
SELECT @NumNodes = COUNT(*) FROM ##Tree
-- Check that at least one node exists
IF @NumNodes < 1
BEGIN
SET @ERROR_MESSAGE = 'Not a tree: There are no nodes'
SET @ERROR_NUMBER = 999
RETURN @ERROR_NUMBER
END
-- Check if NodeId is unique so it can become a primary key
SELECT @COUNT = COUNT(*) FROM (SELECT NodeId FROM ##Tree GROUP BY NodeId) d
IF @COUNT < @NumNodes
BEGIN
SET @ERROR_MESSAGE = 'The column [' + CAST(@NodeId AS VARCHAR(16)) + '] is not unique and cannot become a primary key'
SET @ERROR_NUMBER = 999
RETURN @ERROR_NUMBER
END
-- Ensure that NodeId is not NULLable so it can become a primary key
-- Note that NodeId is INT so @NodeId must convert to INT
ALTER TABLE ##Tree ALTER COLUMN NodeId INT NOT NULL
-- Add primary key using NodeId
SET @SQL = 'ALTER TABLE ##Tree ADD CONSTRAINT PK_NodeId PRIMARY KEY (NodeId);'
EXEC dbo.sp_executeSQL @SQL
/*
Testing ##Tree
*/-- Check that exactly one node has a NULL ParentId (abort otherwise)
SELECT @COUNT = COUNT(*) FROM ##Tree WHERE ParentId IS NULL
IF @COUNT <> 1
BEGIN
SET @ERROR_MESSAGE = 'Not a tree: There are ' + CAST(@COUNT AS VARCHAR(16)) + ' nodes with a NULL ParentId (must be exactly one)'
SET @ERROR_NUMBER = 999
RETURN @ERROR_NUMBER
END
-- Check that each ParentId refers to an existing node (abort otherwise)
SELECT @COUNT = COUNT(*) FROM ##Tree WHERE ParentId NOT IN (SELECT NodeId FROM ##Tree)
IF @COUNT > 0
BEGIN
IF @COUNT > 0 SELECT * FROM ##Tree WHERE ParentId NOT IN (SELECT NodeId FROM ##Tree)
SET @ERROR_MESSAGE = 'Not a tree: There are ' + CAST(@COUNT AS VARCHAR(16)) + ' nodes with an invalid ParentId'
SET @ERROR_NUMBER = 999
RETURN @ERROR_NUMBER
END
-- Arbitrarily set the Id of a fake node.
-- This node will be the parent of the top node so that each node
-- has a parent in the loop below (for convenience).
SET @FakeNodeId = -1 -- Must not be the Id of a real node
/*
The loop below sorts the nodes by the longest path to their leaves.
This sorted list is stored in the temporary table #Height. Since the graph is
finite this loop must terminate within @NumNodes steps unless a loop exists,
so the incrementing number of steps is monitored to prevent an infinite loop.
First create a preorder table #tblPreorder(A,B) that will list the directed edges
between the nodes of the tree (ie. node B is the parent of node A).
Be aware that only the nodes appearing in either column of this table are known
to the loop below. So when that loop deletes all the records from the preorder table
representing directed edges from various nodes to the top node, the top node will
disappear and won't appear in #Height. For that reason a fake edge from the
top node to the fake node is created.
*/-- Drop table #tblPreorder
IF OBJECT_ID(N'tempdb..#tblPreorder') IS NOT NULL DROP TABLE #tblPreorder
-- Add directed edges to #tblPreorder
SELECT NodeId, ParentId
INTO #tblPreorder
FROM ##Tree
-- Count number of edges to be returned by the proc (optional)
SET @ROW_COUNT = @@ROWCOUNT
-- Make the fake node the parent of the top node
UPDATE #tblPreorder
SET ParentId = @FakeNodeId
WHERE ParentId IS NULL
-- Prepare temporary table #Height
IF OBJECT_ID(N'tempdb..#Height') IS NOT NULL DROP TABLE #Height
CREATE TABLE #Height(
NodeId INT,
Height INT
)
/*
Recursively add nodes in column A of the preorder table to #Height if they don't
appear in column B of the preorder table, while deleting the rows of the preorder
table in which they appeared (so we don't do this again). Note that the fake node
guarantees that the top node won't prematurely disappear by earlier deletions,
preventing it from joining #Height with the correct height. Increment the node height
for each step, which cannot exceed the number of nodes since we're starting from 0.
If it does, then a loop exists in the tree so it's not really a tree (the remaining edges in
the preorder table will form the loop in the graph that prevents it from being a tree).
*/PRINT 'Maximum possible height in tree = ' + CAST(@NumNodes - 1 AS VARCHAR(16))
SET @Height = 0
WHILE (SELECT COUNT(*) FROM #tblPreorder) > 0
BEGIN
-- Add nodes in A to #Height that don't appear in B
-- These are the nodes in A that have no children
INSERT INTO #Height(NodeId,Height)
(
SELECT NodeId, @Height AS 'Height'
FROM #tblPreorder
WHERE
NodeId NOT IN (
SELECT ParentId FROM #tblPreorder
)
)
-- Delete rows in #tblPreorder where A doesn't appear in B
-- These are the directed edges for the nodes in A that have no children
-- So on the next step, new nodes will now become childless
DELETE
FROM #tblPreorder
WHERE
NodeId NOT IN (
SELECT ParentId FROM #tblPreorder
)
-- Increment node height for the next step
PRINT 'Height = ' + CAST(@Height AS VARCHAR(16))
SET @Height = @Height + 1
-- Abort if height exceeds the number of nodes (ie. loop exists with remaining edges)
-- List the remaining edges
-- Subtle point: @Height = @NumNodes works for all trees EXCEPT when each node has at most one child
IF @Height = @NumNodes + 1
BEGIN
SELECT * FROM #tblPreorder
SELECT @COUNT = COUNT(*) FROM #tblPreorder
SET @ERROR_MESSAGE = 'Not a tree: One or more loops involving ' + CAST(@COUNT AS VARCHAR(16)) + ' edges exist in tree.'
SET @ERROR_NUMBER = 999
RETURN @ERROR_NUMBER
END
END
/*
At this point @Tree is known to be a tree
Now add and populate additional columns to it that are useful for querying
*/-- Add columns NumDescendants, NumChildren, Height, Depth to ##Tree
ALTER TABLE ##Tree ADD NumDescendants INT NULL
ALTER TABLE ##Tree ADD NumChildren INT NULL
ALTER TABLE ##Tree ADD Height INT NULL
ALTER TABLE ##Tree ADD Depth INT NULL
-- Initialize new columns to 0
UPDATE ##Tree SET NumDescendants = 0, NumChildren = 0, Height = 0, Depth = 0
-- Update NumChildren, NumDescendants by crawling up the tree from its leaves
-- Note that this computation for nodes at each height employs the values of its children
-- That is why an UPDATE is executed at each level, starting from its leaves (Height = 0)
SET @I = 0
WHILE @I < @NumNodes
BEGIN
SET @I = @I + 1
UPDATE g
SET
g.NumChildren = (SELECT count(*) FROM ##Tree i where i.Parentid = g.Nodeid),
g.NumDescendants = (SELECT sum(NumDescendants) FROM ##Tree h where h.Parentid = g.Nodeid) +
(SELECT count(*) FROM ##Tree k where k.Parentid = g.Nodeid)
FROM ##Tree g
WHERE g.NodeId IN (SELECT Nodeid FROM #Height WHERE Height = @I)
END
-- Update Height
UPDATE t
SET t.Height = h.Height
FROM ##Tree t
INNER JOIN #Height h
ON t.NodeId = h.NodeId
-- Update Depth
-- Crawl down the tree from its top node
IF OBJECT_ID(N'tempdb..#Depth') IS NOT NULL DROP TABLE #Depth
;WITH cte (NodeId, Depth) AS (
SELECT NodeId, 0 AS Depth -- Add top node to cte
FROM ##Tree
WHERE NodeId = (SELECT TOP 1 NodeId WHERE ParentId IS NULL)
UNION ALL
SELECT g.NodeId, cte.Depth + 1 AS Depth -- Add children of nodes currently in cte
FROM ##Tree g
INNER JOIN cte ON cte.NodeId = g.ParentId
)
SELECT NodeId, Depth INTO #Depth FROM cte -- Collect all depths into #Depth
UPDATE g
SET g.Depth = h.Depth
FROM
##Tree g INNER JOIN #Depth h
ON g.NodeId = h.NodeId
-- Execute DDL in @DDL
-- Execute @DDL first so @DML sees changes to database structure
IF trim(@DDL) <> ''
BEGIN
PRINT @DDL
EXEC dbo.sp_executeSQL @DDL
END
-- Execute DML in @DML
IF trim(@DML) <> ''
BEGIN
PRINT @DML
EXEC dbo.sp_executeSQL @DML
END
-- Drop global temp table ##Tree
IF OBJECT_ID(N'tempdb..##Tree') IS NOT NULL DROP TABLE ##Tree
END TRY
/*
Error
*/BEGIN CATCH
SET @ERROR_MESSAGE = ERROR_MESSAGE()
SET @ERROR_NUMBER = ERROR_NUMBER()
IF OBJECT_ID(N'tempdb..##Tree') IS NOT NULL DROP TABLE ##Tree
RETURN @ERROR_NUMBER
END CATCH
/*
Normal return
*/SET @ERROR_MESSAGE = ''
SET @ERROR_NUMBER = 0
RETURN @ERROR_NUMBER
END
References
[1] https://en.wikipedia.org/wiki/Topological_sorting
[2] https://www.sqlservercentral.com/articles/ordering-tables-to-preserve-referential-integrity