Summary

Splitting the dataset into a Training set and Test set is one of the basic and essential steps when it comes to test how our machine learning model is performing on a dataset. This helps us determine if the model is able to predict the results or the outcomes. To determine if our model is a best fit for a given data set (that is if it is overfitting or underfitting) then we need to test it on an unseen dataset or a validation dataset. Cross validation is just a technique that sets aside part of our dataset (validation dataset) to evaluate/test the performance of the model and the other part of the dataset other than the reserved one is used for training the model.

In this article, we will look at one of the model selection cum evaluation technique k-Fold Cross Validation, which is used to evaluate our model. It doesn’t necessarily improve the performance of the model, but improves our overall understanding of the model to empower us to make more informed decisions about selecting the most appropriate machine learning model to better explain our dataset and yield more accurate predictions of our result set. Having said that, in this article, we will also look at one of the Performance Boosting technique called XGBoost.

k-Fold Cross Validation Intuition

As explained in the summary, k-Fold Cross Validation is used to evaluate our machine learning model. It can also be used to improve the performance of the model by Parameter Tuning techniques like Random Search or Grid Search, which will be a sequel to this article.

To understand k-Fold Cross Validation, we also need to understand certain concepts like low bias, high bias and variance.

• Low Bias is when our model predictions are very close to the real values.
• High Bias is when our model predictions are far from the real values.
• Low Variance is when we run our model several times, the different predictions of our observation points won’t vary much.
• High Variance is when we run our model several times, the different predictions of our observation points

  will vary a lot.

What we want to get when we build a machine learning model is Low Bias and Low Variance.

k-Fold Cross Validation:

• helps us with model evaluation finally determining the quality of the model.
• is crucial to determining if the model is generalizing well to data.
• checks if the model is overfitting or underfitting.
• lets us choose the model which had the best performance.

Implementing the k-Fold Cross-Validation in Python

The dataset is split into ‘k’ number of subsets. k-1 subsets then are used to train the model, and the last subset is kept as a validation set to test the model. Then the score of the model on each fold is averaged to evaluate the performance of the model.

To implement the k-Fold Cross Validation we will use the same sample 'Beer' dataset as demonstrated in the prequel to this article. First we import the necessary Python Modules into the IDE (Integrated Development Environment). Here we are using Jupyter Lab of Anaconda Distribution.

# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

Next, we import the file named 'BeerDataset.csv' in the below step.

# Importing the dataset
dataset = pd.read_csv('BeerDataset.csv')

In the below code snippet, we read the columns from the 1st to the 12th of this 'BeerDataset' (the independent variables of this dataset) and assign it to 'X', which is a numpy array. Similarly we parse the result column of the dataset, which is the 'Beer_Grade' (the dependent variable), and assign it to 'Y', which is also a numpy array. Then we print the output and the type of variables 'X' and 'Y' as shown below.

# Assigning the Independent Variables to "X" and Dependent Variable Column to "y"
X = dataset.iloc[:, 0:13].values
y = dataset.iloc[:, 13].values

The next step would be divide the dataset into the training set and the test set. The training set is a subset of our data on which our model will learn how to predict the dependent variable with the independent variables. The test set is the complimentary subset from the training set, on which we will evaluate our model to see if it manages to predict correctly the dependent variable with the independent variables.

It is always a recommended practice to split the data into X_train, y_train and X_test, y_test to apply the resampling method(k-Fold) instead of applying it directly on X and y. We can do both, although we can also perform k-fold Cross-Validation on the whole dataset (X, y).

The ideal method is:

1. Split your dataset into a training set and a test set.

2. Perform k-fold cross validation on the training set.

3. Make the final evaluation of your selected model on the test set.

The code snippet for dividing the dataset into Training and Test Set is as shown below:

# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)

Here we are splitting the dataset in the ratio of 3:1 that is 75% of this dataset if the training dataset and 25% of the dataset is the test set. Hence we have the parameter test_size=0.25 within the train_test_split function imported from the sklearn.model selection library.

Next, we do feature scaling on the dataset. Feature Scaling techniques like normalization and standardization are used to normalize the range of independent variables or features of our dataset in order to avoid the results being skewed (biased) when dealing with multiple features spanning varying degrees of magnitude, range, and units. The steps from feature scaling till applying the dimensionality reduction technique of PCA is the same as illustrated in the prequel to this article and can be found here.

In the prequel to this article, we used the 'Logistic Regression' classifier as the machine learning model on which we were training our dataset and then we used the trained dataset to predict the results of an unknown dataset (part of the original dataset itself). Here, we will look at another classifier technique called the kernel-SVM. Support Vector Machine (SVM) is a linear model. We can deduce that easily when visualizing the results on the graph where we will notice that the prediction boundary is a straight line. However, we can make the SVM a non linear model, by adding a kernel, which is called the Kernel-SVM.

Kernel SVM Intuition

In SVM and Kernel SVM we see see the support vectors as vectors and not as points, but in real-world problems we have data-sets of higher dimensions. In this example, the vectors are points in 2-D space. In an n-dimensional space, vectors make more sense and it is easier to do vector arithmetic and matrix manipulations rather than considering them as points. This is why we generalize the data-points to vectors. This also enables us to think of them in an N-dimensional space.

Though in Kernel SVM , we do need to be cognizant of the fact that we need to convert the high dimensional space in 3D back to 2D because we need to go back to our original space that contains our independent variables. If we stayed in the 3d space we would then lose the information of our independent variables because in this 3d space there are not our original independent variables but the projections of them. So we want to go back to the original 2d space by projecting back the points.

Which Kernel to choose?

A good way to decide which kernel is the most appropriate is to make several models with different kernels, and then evaluate each of their performance, and finally compare the results. Then we choose the kernel with the best results. Be careful though, to evaluate the model performance on new observations (preferably with k-Fold Cross Validation that we will discuss below) and to consider different metrics (Accuracy, F1 Score, precision etc.).

Then the code snippet for the kernel-SVM would be as shown below:

# Fitting Kernel SVM to the Training set
from sklearn.svm import SVC
classifier = SVC(kernel = 'rbf', random_state = 0)
classifier.fit(X_train, y_train)

In the above code we have used RBF Kernel (radial basis function). We will test out the model performance on new observations using the k-Fold Cross Validation technique by considering metrics such as mean and standard deviation of the accuracies.

The fit method in the above code snippet will simply train the SVM model on X_train and y_train with a non linear Kernel. More precisely, the fit method will collect the data in X_train and y_train, and from that it will do all successive operations. This method will first perform a mapping in a higher dimensional space where the data is linearly separable, then compute the support vectors in this higher dimensional space, and eventually create a projection back into 2D.

Right after the code computes the support vectors we have a 'Kernel - SVM'  classifier model fully trained on our training data, and ready to predict new predictions with the predict method, which is demonstrated in the below script.

# Predicting the Test set results
y_pred = classifier.predict(X_test)

We can calculate the confusion matrix and the code for confusion matrix is the same as we have seen in the prequel to this article, which can be found here.

Although, Confusion Matrix  is not the optimal way to evaluate the performance of the model, it just gives us an idea of how well our model can perform. If we get a good confusion matrix with few prediction errors on the test set, then there is a chance our model has a good predictive power. However the most relevant way to evaluate our model is through K-Fold Cross Validation. It consists of evaluating our model on several test sets (called the validation sets), so that we can make sure we don’t get lucky on one single test set. Today most Data Scientists or AI Developers evaluate their model through k-Fold Cross Validation.

The code to implement the k-Fold Cross Validation technique is as shown below:

# Applying k-Fold Cross Validation
from sklearn.model_selection import cross_val_score
accuracies = cross_val_score(estimator = classifier, X = X_train, y = y_train, cv = 10)

In the above code snippet, cross_val score is a method which we import from sklearn.model_selection module to evaluate a score by cross-validation.

• estimator: object implementing ‘fit’.  The object to use to fit the data.
• X array-like of shape. The data to fit.
• y array-like of shape. The target variable to try to predict in the case of supervised learning.
• cv integer, cross-validation generator, default=None (uses the default 5-fold cross validation). Determines the cross-validation splitting strategy. To specify the number of folds we specify cv an an integer. In our code it is 10.

As mentioned earlier, the dataset here is split into ‘k’ number of subsets. The ideal/best value of k to choose when performing k-Fold Cross Validation is 10. Since we will be evaluating our model on 10 different subsets (the ten test set folds in the cross-validation process), we will then have a good analysis on the performance of the machine learning model in predicting the outcomes of the result dataset and we would then have no stone left unturned in our evaluation of the model. The metrics derived from such an analysis will then empower us to make data driven decisions of choosing one machine learning model over an another.

We can then use the following metric depicted in the code snippet below to explain the evaluation of this classifier machine learning model 'Kernel - SVM'.

# Calculating the mean  and Standard Deviation of the 'Accuracy' Metric
accuracies.mean()
accuracies.std()

The mean accuracy resulting from all the 10 validation datasets is 96.6%.

Similarly the Standard Deviation  of the accuracies resulting from these 10 validation datasets is 4.5%.

Through k-Fold Cross Validation, we need to estimate the "unbiased error" on the dataset from this model. The mean is a good estimate of how the model will perform on the dataset. Then once we are convinced that the average error is acceptable, we train the same model on all of the dataset.

The Standard Deviation of the model’s accuracy simply shows that the variance of the model accuracy is 4.5%. This means the model can vary about 4.5%, which means that if we run our model on new data and get an accuracy of 96.6%, we know that this is like within 92.1 to 100% accuracy. Bias and accuracy sometimes don’t have an obvious relationship, but most of the time we can spot some bias in the validation or testing of our model when it does not preform properly on new data.

Next, if we visualize the results of the training set results using the below snippet of code:

# Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                     np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
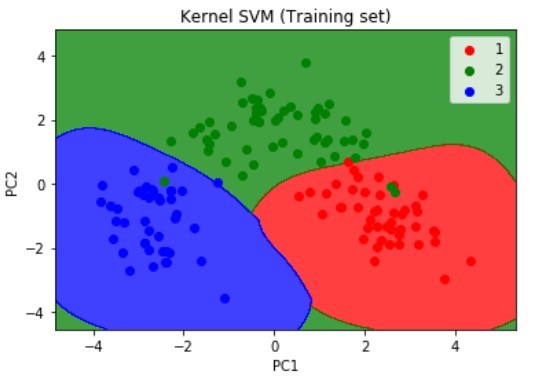
plt.title('Kernel SVM (Training set)')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legend()
plt.show()

As mentioned earlier we can make the SVM a non linear model, by adding a kernel, and as we can deduce from the  visualization results on the graph that the prediction boundary is a curve.

Similarly using the below code when we visualize the results of the Test set results we get the graph as illustrated below:

# Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                     np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
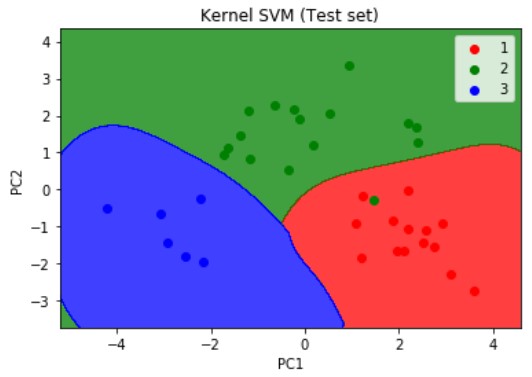
plt.title('Kernel SVM (Test set)')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legend()
plt.show()

Performance Boosting Technique - XGBoost

'Boosting' Algorithms are one of the most widely used algorithms and they basically grant power to machine learning models to improve their accuracy of prediction. Boosting is an ensemble technique where new models are added to correct the errors made by existing models. Models are added sequentially until no further improvements can be made. 'It can be refereed to as a family of algorithms which converts weak learners (weak prediction models) to strong learners(strong prediction models). There are many boosting algorithms such as AdaBoost (Adaptive Boosting), Gradient Tree Boosting, XGBoost. In this article, we will focus on XGBoost followed by its Python code which is a great all-round algorithm worth having in a Data Scientist's/AI Developer's tool box.

XGBoost stands for eXtreme Gradient Boosting. XGBoost is a software library that we can download and install on our machine, then access from a variety of interfaces like CLI (Command Line Interface), C++, Python interface, R Interface etc. XGBoost library is laser focused on computational speed and model performance and it offers some advanced features also with respect to model features, system features and algorithm features for achieving higher efficiencies in compute time, memory resources and for use in a range of computing environments. The XGBoost library implements the gradient boosting decision tree algorithm. It is called gradient boosting because it uses a gradient descent algorithm to minimize the loss when adding new models.

XGBoost dominates the structured data or tabular datasets on classification and regression techniques of predictive modeling problems. On a side note, it is the defacto or the go to algorithm used by many winners on Kaggle Competitive Data Science platform.

For the Python code of XGBoost we follow the same steps as outlined in the prequel to this article from Importing the libraries and the 'Beer' Dataset.

# Fitting XGBoost to the Training set
 
from xgboost import XGBClassifier
classifier = XGBClassifier()
classifier.fit(X_train, y_train)

If you have trouble installing the XGBoost package use the following snippet of code in the cell of Jupyter Notebook, the IDE we are using throughout this article for our Python code demonstration. Run the below script before running the actual XGBoost code shown above.

#Python Script for Installing the 'XGBoost' inside the cell of Juypter Notebook IDE of Anaconda Distribution
import sys
!{sys.executable} -m pip install xgboost

Alternatively, if you are using any other IDE, we need to enter the following command inside a terminal (or anaconda prompt for Windows users)

#Python Script for Installing the 'XGBoost' inside the Python terminal
conda install -c conda-forge xgboost

We can then repeat the steps as outlined in the k-Fold Cross Validation section of this article from 'Predicting the Test set results' to calculating the mean and standard deviation of accuracies. For clarity purposes the code is illustrated once again followed by its output.

# Predicting the Test set results
y_pred = classifier.predict(X_test)
# Making the Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
# Printing the Confusion Matrix
cm
# Applying k-Fold Cross Validation
from sklearn.model_selection import cross_val_score
accuracies = cross_val_score(estimator = classifier, X = X_train, y = y_train, cv = 10)
accuracies.mean()
accuracies.std()

The mean accuracy resulting from all the 10 validation datasets after applying the XGBClassifier() is  97.2%.

Similarly the Standard Deviation  of the accuracies resulting from these 10 validation datasets is 3.4%.

Conclusion

In this article, we have seen how we can use k-Fold Cross Validation ( a model selection technique) to evaluate our machine learning model  used to perform prediction on our actual dataset. As stated earlier, it doesn’t necessarily improve our model, but improves our overall understanding of the model. However we can use it to improve the performance of our machine learning model by combining it with some Parameter Tuning techniques like Grid Search which we will look in the sequel to this article.

Next Steps

As stated earlier, in the sequel to this article, we will be looking at:

• Performance Tuning techniques like Grid Search and how it can be used to improve the performance of our machine learning model.
• Watch out for an upcoming article on step by step code on how to apply various Regression, Classification, Clustering, Association Rule Learning, Reinforcement Learning, NLP and Deep Learning techniques using Python where we will look at some of the most popular techniques and how to evaluate thier performance.
• For more examples on sample dataset pre-processing steps to prepare the data for more deeper structured analysis read my article on 'Comparing Two Geospatial Series with Python' and 'Reading a Specific File from an S3 bucket Using Python'.
• To gain a holistic overview of how Diagnostic, Descriptive, Predictive and Prescriptive Analytics can be done using Geospatial data, read my recent paper, which has been published on advanced data analytics use cases pertaining to that.