The RAND() function presents developers with a trap for the unwary. According to the latest edition of Books Online it "produces a pseudo-random number in the range 0 to 1, exclusive".
As a statement this is not a universal truth, it is only true from certain perspectives.
In this article I am going to use the Adventureworks2014 database to demonstrate the pitfalls of the RAND() statement.
PROBLEM ONE: Random numbers over a batch
If we use RAND() without a seed value then a single "random" value will be generated across the entire result set and not a random value per record.
SELECTRandomValue=RAND()FROMperson.StateProvince
At least if we run the above query again we will get a different RandomValue, which is more than can be said for specifying a specific seed
SELECTRandomValue=RAND(32768)FROMperson.StateProvince
The query above generates the value 0.324138575220812 for every record on all the machines I have available to me. This tells me that for a given seed the random number algorithm is a deterministic function.
Finally, whatever the formula the RAND() function uses it is clearly symmetrical around zero. The following query will produce two identical values.
SELECT RAND(32768),RAND(-32768)In short RAND() does not appear to have been designed with set based operations in mind.
PROBLEM TWO: RAND() for sequential seeds is definitely not random
The query below demonstrates just how poor the RAND() function is.
SELECTRandomValue=RAND(StateProvinceID),StateProvinceIDFROMperson.StateProvinceORDER BY1-- Order by the allegedly random value
If RAND() was truly random I would expect the StateProvinceID records to be randomly ordered however this is clearly not the case.
Plotting the values on a graph and adding a linear trend line emphasizes this fact.
For those of you not familiar with linear regression the R2 value measures the goodness of fit between the data sample and the calculated trend line. A value of 1 represents a perfect fit.
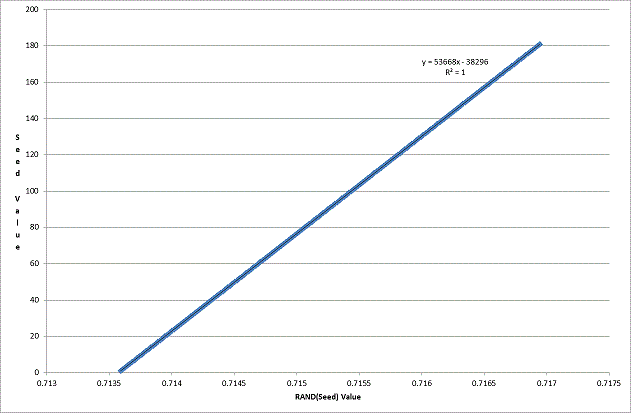
I decided to explore this observation a bit further as Person.StateProvince is quite a small set of data.
Preparing Adventureworks2014 for experimentation
I expanded the database and log file each to 1GB so that I could create my test data.
When I experiment I use SQLCMD mode as this allows me to parameterise what I am trying to do to a greater extent than T-SQL variables normally allow. SQLCMD mode can be switched on from the "Query" menu and appears near the bottom of the screen as cir led in RED below
The snippet of code below ensures that the recovery model for the database is set to SIMPLE and prints a confirmation message just to be sure.
:setvar DB Adventureworks2014USE$(DB)GO IFEXISTS(SELECT1FROMsys.databasesWHEREname ='$(DB)'AND recovery_model_desc<>'SIMPLE')BEGIN ALTER DATABASE$(DB) SET RECOVERY SIMPLE'DB RECOVERY MODEL CHANGED: SIMPLE'END GO DECLARE@RecoveryModelNameNVARCHAR(120)SELECT@RecoveryModelName=recovery_model_descFROMsys.databasesWHEREname ='$(DB)'RAISERROR('DB RECOVERY MODEL FOR $(DB) = %s',10,1,@RecoveryModelName)WITH NOWAITGO
The next step is to create a table to hold a large number of seed values and their associated RAND() value.
IFEXISTS(SELECT1FROMsys.objectsWHEREobject_id=OBJECT_ID('dbo.RandomTest'))BEGIN DROP TABLEdbo.RandomTest'TABLE DROPPED: dbo.RandomTest'END GO CREATE TABLEdbo.RandomTest ( SeedValueINTNOT NULLCONSTRAINTPK_RandomTestPRIMARY KEY CLUSTERED, RANDNumberFLOATNULL )GO
Populating the dbo.RandomTest table
We want to generate a respectable number of seed values and their associated RAND() values.
The use of a cross join on sys.columns is a useful way of generating a large number of records. If there are 2,000 records in sys.columns then the cross join will produce 2,000 x 2,000 = 4,000,000 records.
The query below makes use of the cross join trick in the Common Table Expression (CTE) but caps the number of records used to 1 million in the query that consumes the CTE.
--Populate our experiment tableWITHcte(SequentialNumber)AS(SELECTROW_NUMBER()OVER(ORDER BYC1.Column_Id)FROMsys.columnsASC1,sys.ColumnsASC2 )INSERT INTOdbo.RandomTest (SeedValue,RANDNumber)SELECT TOP1000000 SequentialNumber,RAND(SequentialNumber)FROMcteGO CHECKPOINT GO
Evaluating the results
I wanted to gain some form of metric for the relationship between the seed value and its associated RAND() value.
I wanted to compare the random number generated for a seed with that of the next sequential seed. If the current random value is less than the next random value then I wanted to count those occurrences.
WITHcte(Seed1, Seed2, InOrder)AS(SELECTA.SeedValue, B.SeedValue,CASE WHENA.RANDNumber<B.RANDNumberTHEN1ELSE0ENDFROMdbo.RandomTestASA LEFT JOIN dbo.RandomTestASBONA.SeedValue = B.SeedValue-1 )SELECTOutOfOrder=COUNT(*)-COUNT (NULLIF(InOrder,1)), InOrder=COUNT(*)-COUNT (NULLIF(InOrder,0))FROMcteGO
- NULLIF returns a NULL value if all arguments are equal
- COUNT will only count the non-null values.
My query returned the following result set.
OutOfOrder | InOrder |
20 | 999,980 |
Implications of ordered random numbers
Clearly RAND() produces a value that is highly correlated with its seed.
Back in the days of the Commodore VIC20 the trick to getting the BASIC RND() function to produce a decent sequence of random numbers was to seed it with a timer value.
The equivalent .NET function also defaults to using a timer based seed when no seed is specified.
The T-SQL equivalent clearly will not work on two fronts:-
- The correlation with the sequential seed as described above
- The conversion of CURRENT_TIMESTAMP (or GETDATE()) to a seed value is simply too coarse grained.
Consider the query below:
SELECTCAST(CURRENT_TIMESTAMPAS FLOAT)
- The integer portion of the value represents the days elapsed since 1st January 1900.
- The decimal portion is a fraction of a day.
To keep the value within the bounds of a 32 bit integer we can multiply timestamp value by 10,000. This allows us to make use of up to 4 decimal places.
0.001 of a day = 8.64 seconds. Even if sequential seeds did produce a random distribution we would still not be able to use the timer unless we only generated a number every 8.6 seconds!
Does the .NET framework offer a better solution?
The short answer is NO. To test the .NET ability to generate random numbers from sequential seed values I wrote a short console application and noticed something peculiar. It appeared that odd seeds were following a pattern and even seeds were following a similar but separate pattern.
usingSystem;namespaceRandomExperiment {classProgram {static voidMain(string[] args) {for(inti = 0; i < 200; i+=2) { Console.Write(" {0,10} ", new Random(i).Next()); Console.Write(" {0,10} ", new Random(i+1).Next()); Console.WriteLine(); }strings=Console.ReadLine(); } } }
The graph below shows the output from the program.
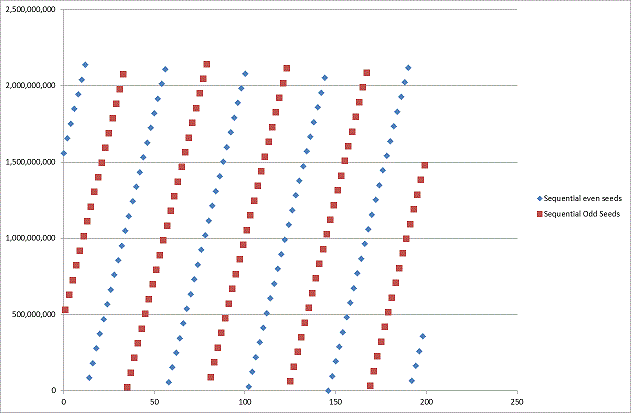
Clearly there is a strong pattern
How about repeated calls to RAND()
In no way conforming to the stereotype of an IT geek playing Dungeons and Dragons I am going to test the randomness of the RAND function by simulating a 10 sided dice and by generating 100,000 roles of that dice.
To determine whether our dice are biased a little bit of knowledge of the binomial distribution should help.
If RAND() is unbiased then I would expect approximately 10,000 incidents of each dice face. I would expect some faces to appear slightly more and others slightly less than 10,000 but not significantly.
V = np(1-p)
Variance = Number of Roles x Probability of getting a particular face x probability of not getting a face.
V= 100,000 x 0.9 * 0.1 = 9,000
Standard Deviation = Square Root of the Variance = 94.87.
The normal distribution tells us that a certain number of standard deviations either side of the mean describes the probability of the dice being biased.
Confidence level | Number of standard deviations | Leeway either side | Low Occurrence | High Occurrence |
90% | 1.64 | 156 | 9,844 | 10,156 |
95% | 1.96 | 186 | 9,814 | 10,186 |
99% | 2.58 | 245 | 9,755 | 10,245 |
In other words if we wanted to be 99% confident that a dice was biased we would expect a particular face to crop up outside the range of 9,844 and 10,156 times.
So let us turn that into SQL code.
IFEXISTS(SELECT1FROMsys.objectsWHEREobject_id=OBJECT_ID('dbo.RepeatedRand') AND type='U')BEGIN DROP TABLEdbo.RepeatedRand'TABLE DROPPED: dbo.RepeatedRand'END GO CREATE TABLEdbo.RepeatedRand ( RepeatedRandIDINTNOT NULLIDENTITY(1,1)CONSTRAINTPK_RepeatedRandPRIMARY KEY CLUSTERED, RandValueTINYINTNOT NULLCONSTRAINTDF_RepeatedRand_RandValueDEFAULT(CAST(10*RAND()AS INT)) )GO SETNOCOUNT ON-- Generate 100,000 recordsINSERT INTOdbo.RepeatedRandDEFAULT VALUES GO100000
To measure the number of occurrences of each value we run the simple query shown below.
SELECTRandValue,NumberOfOccurrences=COUNT(*)FROMdbo.RepeatedRandGROUP BYRandValueORDER BYRandValue
Your results will vary on each run. The table below shows a result set I received.
RandValue | NumberOfOccurrences |
|---|---|
0 | 9,979 |
1 | 9,932 |
2 | 9,909 |
3 | 10,127 |
4 | 9,971 |
5 | 9,915 |
6 | 10,075 |
7 | 9,960 |
8 | 10,001 |
9 | 10,131 |
As all values are within the 9,844 to 10,156 range I can be sure that there is no particular bias towards one number.
However, that is not the whole story. The numbers picked may comply with a uniform distribution but what about when they are picked?
If the choosing of numbers is random then from our 100,000 sample we would expect the following:-
- Approximately 45,000 numbers to be lower than the preceding number
- Approximately 10,000 numbers to be the same as the preceding number
- Approximately 45,000 numbers to be higher than the preceding number
The SQL Query to measure this is as follows:-
;WITHcte(Seed1, Seed2, InOrder)AS(SELECTA.RepeatedRandId, B.RepeatedRandId,CASE WHENA.RANDValue<B.RANDValueTHEN-1WHENA.RandValue>B.RandValueTHEN1WHENA.RandValue=B.RandValueTHEN0ELSE2ENDFROMdbo.RepeatedRandASA LEFT JOIN dbo.RepeatedRandASB ON A.RepeatedRandId = B.RepeatedRandId-1 )SELECTLessThan=COUNT(*)-COUNT (NULLIF(InOrder,-1)), Equal=COUNT(*)-COUNT (NULLIF(InOrder,0)) , WTF=COUNT(*)-COUNT (NULLIF(InOrder,2)) , MoreThan=COUNT(*)-COUNT (NULLIF(InOrder,1))FROMcteGO
An example of a result set I got is shown below:-
LessThan | Equal | WTF | MoreThan |
|---|---|---|---|
44974 | 9962 | 1 | 45063 |
Note that the WTF captures the last LEFT record for which there is no RIGHT equivalent.
Again, this shows that the appearance of values is unbiased.
The work around to make RAND() work with sets
To recap the problem with the RAND() function is that it does not appear to be designed with set based operations in mind.
This presents database developers with a paradox. To produce random numbers over a set it needs to be seeded with random numbers in the first place. This is somewhat of a chicken and egg scenario.
The general solution used involves CHECKSUM() and NEWID(). For example
SELECTRAND(CHECKSUM(NEWID()))FROMperson.StateProvince
It works as follows:-
- The nearest we have to a random value is a unique identifier as generated by the NEWID() function.
- RAND needs an integer value for its seed. By using the CHECKSUM() value of our NEWID() we achieve our goal.
- RAND produces a identical value for a given integer regardless of its sign (positive or negative)
What are we trying to do with RAND() anyway?
Choosing records at random
If we are trying to choose random records from a table then there are a couple of approaches covered by the MSDN article from 2008 by Marcelo De Barros, Kenton Gidewall.
For small to medium tables the following query is adequate
SELECT TOP10 *FROMPerson.StateProvinceORDER BYNEWID()
As illustrated in their article, once the number of records gets beyond a certain point then this method becomes progressively more expensive.
For large tables Marcelo De Barros and Kenton Gidewall's more creative approach offers an higher performance approximation
SELECT*FROMPerson.StateProvinceWHERE(ABS(CAST((BINARY_CHECKSUM(*) * RAND())ASINT)) % 100) < 10
The way that this works is as follows:-
- BINARY_CHECKSUM(*) creates a signed 32 bit integer value as a check sum across the record.
- RAND() produces a single random value across all records but when multiplied by the BINARY_CHECKSUM the result does produce the appearance of randomness
- ABS turns this into a signed value
- %100 returns the modulus (remainder) when the values above are divided by 100
- <10 Gives us the remainders that are 0 to 9 or 10 percent of the recordset.
The De Barros and Gidewall approach works best with tables with a large number of rows and also a large number of varying columns.
Generating test data and/or running simulations
Personally I would sooner research and buy a tool to achieve data generation or for producing simulations.
Producing a decent tool for either situation is a skilled and time-consuming job. It is easy for an IT person to cost £300/day or more so these tools are worthwhile on two fronts:-
- IT staff time/cost saved
- A good simulation can tease out bugs and realistic performance issues early. Avoidance is cheaper than fixing.
I would sooner be able to say "Our simulation shows that we are likely to get a problem in scenario 'x', let's think about the possible ways to avoid the scenario" than be in the thick of a production incident trying to put in a sticking plaster solution.
For general data generation Red-Gate Data Generator offers a decent feature set and works well and handles data referential integrity well.
Simulations are a trickier area and are usually in the province of statistical software packages
Concluding thoughts
Random number generation or utilisation is not something I have used often within a database. There are practises that today we class as anti-patterns as better thought through approaches exist. Yesterday the approaches had yet to emerge and our anti-pattern practises were all that we had. There are always exceptions where the use of a pattern may be appropriate but I suspect the use of RAND() is one that leans towards being an anti-pattern.


