Everybody has at one time in his life, had experience with recursion. When I
was young, I was on leave in Paris in an old building in which the corridor had
two mirrors facing each other. When I passed between theses mirrors my body was reflected ad infinitum, and I was very proud, joyfully admiring my image and having a concrete view of what is the infinite. That is it : recursion... A process which is able to reproduce himself for some period of time.
In mechanical situations, we do not accept infinite recursion. In the real world, we must have a stopping point because our universe is closed. Waiting for the end of an infinite process, which in fact is eternity, is a hard job ! As Woody Allen says : "eternity is really long, especially near the end ..."
In computer management, recursion is a special technique that is able, sometimes, to treat complex algorithms with an elegant coding style : a few lines will do a complete job. But recursion has some perverse effects : the resources to do the job are maximized by the fact that every call of the embedded process needs to open a complete environment space, which has the effect of using a large volume of memory. A mathematician, whose name I cannot recall, says that every recursive algorithm can be reduce to an iterative one by the use of a stack!
But our purpose in this article is to speak about RECURSIVE QUERIES in SQL, regarding the ISO standard and what MS SQL Server 2005 has done with it.
The ISO SQL:1999 standard
Here is the short syntax of a RECURSIVE QUERY :
WITH [ RECURSIVE ] <query_alias_name> [ ( <column_list> ) ] AS ( <select_query> ) <query_using_query_alias_name>
Simple ! Isn't it? In fact, all the mechanics are inside the <select_query>. We will
show first simple, but not recursive queries, and when we understand what we can do with the keyword WITH, we will tear down the curtain to see how sexy recursion is in SQL.
A simple CTE
The use of only the WITH clause (without the keyword RECURSIVE), is to build a Common Table Expression (CTE). In a way CTE is a view build especially for a query and used in one shot: each time we execute the query. In one sense it can be called a "non persistent view".
The basic use of a CTE is to make clear some expression that contains a query twice or more in a complex query. Here is a basic example :
-- if exists, drop the table we need for the demo
IF EXISTS (SELECT *
FROM INFORMATION_SCHEMA.TABLES
WHERE TABLE_SCHEMA = USER
AND TABLE_NAME = 'T_NEWS')
DROP TABLE T_NEWS
GO
-- create the table
CREATE TABLE T_NEWS
(NEW_ID INTEGER NOT NULL PRIMARY KEY,
NEW_FORUM VARCHAR(16),
NEW_QUESTION VARCHAR(32))
GO
-- population
INSERT INTO T_NEWS VALUES (1, 'SQL', 'What is SQL ?')
INSERT INTO T_NEWS VALUES (2, 'SQL', 'What do we do now ?')
INSERT INTO T_NEWS VALUES (3, 'Microsoft', 'Is SQL 2005 ready for use ?')
INSERT INTO T_NEWS VALUES (4, 'Microsoft', 'Did SQL2000 use RECURSION ?')
INSERT INTO T_NEWS VALUES (5, 'Microsoft', 'Where am I ?')
-- the traditionnal query :
SELECT COUNT(NEW_ID) AS NEW_NBR, NEW_FORUM
FROM T_NEWS
GROUP BY NEW_FORUM
HAVING COUNT(NEW_ID) = ( SELECT MAX(NEW_NBR)
FROM ( SELECT COUNT(NEW_ID) AS NEW_NBR, NEW_FORUM
FROM T_NEWS
GROUP BY NEW_FORUM ) T )
-- the result :
NEW_NBR NEW_FORUM
----------- ----------------
3 Microsoft
This query is one that is very popular in many forums, that is, the one that often has the most of number of questions. Tobuild the query, we need to make a MAX(COUNT(... which is not allowed, and so it must be solved through the use of subqueries. But in the above query, there are two SELECT statements, which are exactly the same :
SELECT COUNT(NEW_ID) AS NEW_NBR, NEW_FORUM FROM T_NEWS GROUP BY NEW_FORUM
With the use of a CTE, we can now make the query more readable :
WITH
Q_COUNT_NEWS (NBR, FORUM)
AS
(SELECT COUNT(NEW_ID), NEW_FORUM
FROM T_NEWS
GROUP BY NEW_FORUM)
SELECT NBR, FORUM
FROM Q_COUNT_NEWS
WHERE NBR = (SELECT MAX(NBR)
FROM Q_COUNT_NEWS)
In fact, we use the non persistent view Q_COUNT_NEWS introduced by the WITH expression, to write a more elegant version of the solution of our problem. Like a view, you must name the CTE and you can give new names to columns that are placed in the SELECT clause of the CTE, but this is not an obligation.
Note the fact, that you can use two, three or more CTE to build a query... Let us see an example:
WITH
Q_COUNT_NEWS (NBR, FORUM)
AS
(SELECT COUNT(NEW_ID), NEW_FORUM
FROM T_NEWS
GROUP BY NEW_FORUM),
Q_MAX_COUNT_NEWS (NBR)
AS (SELECT MAX(NBR)
FROM Q_COUNT_NEWS)
SELECT T1.*
FROM Q_COUNT_NEWS T1
INNER JOIN Q_MAX_COUNT_NEWS T2
ON T1.NBR = T2.NBR
This gives the same results as the two prior versions! The first CTE, Q_COUNT_NEWS, is used as a table in the second and the two CTEs are joined in the query to give the result. Note the comma which separates the two CTEs.
3 - Two Tricks for Recursion
To do recursion, the SQL syntax needs two tricks :
FIRST : you must give a starting point for recursion. This must be done by a two part query. The first query says where to begin, and the second query says where to go to next step. These two queries are joined by a UNION ALL set operation.
SECOND : you need to make a correlation between the CTE and the SQL inside the CTE (Inside out, outside in, was a popular disco song ... isn't it ? ) to progress step by step. That is made by referencing the <query_alias_name> inside the SQL that builds the CTE.
4 - First example : a simple hierarchy
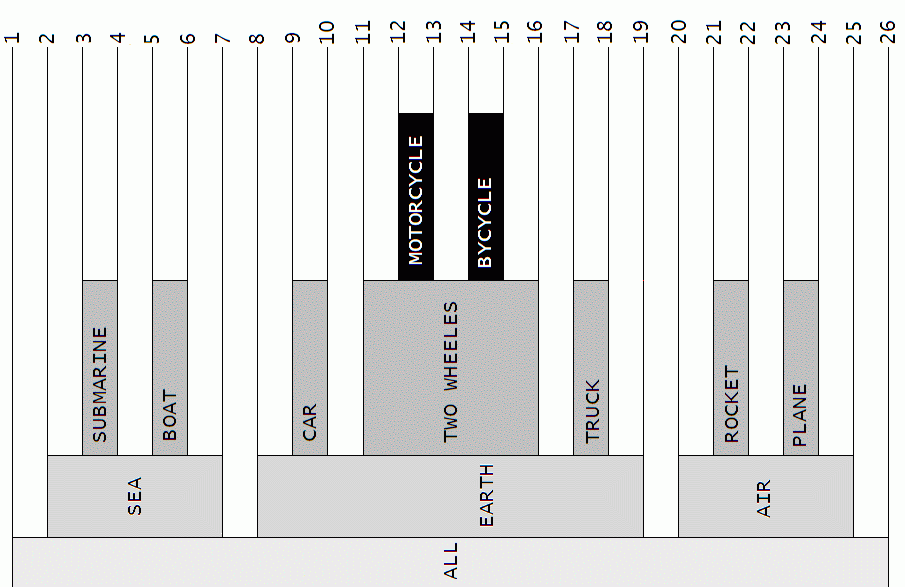
For this example, I have made a table which contains a typology of vehicles :
-- if exists, drop the table we need for the demo
IF EXISTS (SELECT *
FROM INFORMATION_SCHEMA.TABLES
WHERE TABLE_SCHEMA = USER
AND TABLE_NAME = 'T_VEHICULE')
DROP TABLE T_VEHICULE
-- create it
CREATE TABLE T_VEHICULE
(VHC_ID INTEGER NOT NULL PRIMARY KEY,
VHC_ID_FATHER INTEGER FOREIGN KEY REFERENCES T_VEHICULE (VHC_ID),
VHC_NAME VARCHAR(16))
-- populate
INSERT INTO T_VEHICULE VALUES (1, NULL, 'ALL')
INSERT INTO T_VEHICULE VALUES (2, 1, 'SEA')
INSERT INTO T_VEHICULE VALUES (3, 1, 'EARTH')
INSERT INTO T_VEHICULE VALUES (4, 1, 'AIR')
INSERT INTO T_VEHICULE VALUES (5, 2, 'SUBMARINE')
INSERT INTO T_VEHICULE VALUES (6, 2, 'BOAT')
INSERT INTO T_VEHICULE VALUES (7, 3, 'CAR')
INSERT INTO T_VEHICULE VALUES (8, 3, 'TWO WHEELES')
INSERT INTO T_VEHICULE VALUES (9, 3, 'TRUCK')
INSERT INTO T_VEHICULE VALUES (10, 4, 'ROCKET')
INSERT INTO T_VEHICULE VALUES (11, 4, 'PLANE')
INSERT INTO T_VEHICULE VALUES (12, 8, 'MOTORCYCLE')
INSERT INTO T_VEHICULE VALUES (13, 8, 'BYCYCLE')
Usually a hierarchy must be schematized with an auto reference, which is the case here : a foreign key references the primary key of the table. Theses data can be viewed as :
ALL |--SEA | |--SUBMARINE | |--BOAT |--EARTH | |--CAR | |--TWO WHEELES | | |--MOTORCYCLE | | |--BYCYCLE | |--TRUCK |--AIR |--ROCKET |--PLANE
Now let us construct the query. We want to know where does the MOTORCYCLE come from. In other word, what are all the ancestors of "MOTORCYCLE". We must start with the data of the row which contain the motorbyke :
SELECT VHC_NAME, VHC_ID_FATHER FROM T_VEHICULE WHERE VHC_NAME = 'MOTORCYCLE'
We need to have the father ID to go to next step. The second query, which does the next step, must be written like this :
SELECT VHC_NAME, VHC_ID_FATHER FROM T_VEHICULE
As you see, there is no difference between the two queries, except that we do not specify the filter WHERE to go to next step. Remember that we need to join thoses two queries by a UNION ALL, which will specify the stepping method :
SELECT VHC_NAME, VHC_ID_FATHER FROM T_VEHICULE WHERE VHC_NAME = 'MOTORCYCLE' UNION ALL SELECT VHC_NAME, VHC_ID_FATHER FROM T_VEHICULE
Now let us place this stuff in the CTE :
WITH
tree (data, id)
AS (SELECT VHC_NAME, VHC_ID_FATHER
FROM T_VEHICULE
WHERE VHC_NAME = 'MOTORCYCLE'
UNION ALL
SELECT VHC_NAME, VHC_ID_FATHER
FROM T_VEHICULE)
Now we are close to the recursion. The last step is to make a cycle to execute the stepping techniques. This is done by using the CTE name as a table inside the SQL of the CTE. In our case, we must join the second query of the CTE to the CTE itself, by the chain made with tree.id = (second query).VHC_ID. This can be realized like this :
WITH
tree (data, id)
AS (SELECT VHC_NAME, VHC_ID_FATHER
FROM T_VEHICULE
WHERE VHC_NAME = 'MOTORCYCLE'
UNION ALL
SELECT VHC_NAME, VHC_ID_FATHER
FROM T_VEHICULE V
INNER JOIN tree t
ON t.id = V.VHC_ID)
SELECT *
FROM tree
There is nothing more to do other than make the select as simple as possible to show the data. Now, if you press the F5 button to execute... You will see this :
data id ---------------- ----------- MOTORCYCLE 8 TWO WHEELES 3 EARTH 1 ALL NULL
Now have a look back at the relationships that do the stepping, in a graphic view :
correlation
____________________________________
| |
v |
WITH tree (data, id) |
AS (SELECT VHC_NAME, VHC_ID_FATHER |
FROM T_VEHICULE |
WHERE VHC_NAME = 'MOTORCYCLE' |
UNION ALL |
SELECT VHC_NAME, VHC_ID_FATHER |
FROM T_VEHICULE V |
INNER JOIN tree t <---------------
ON t.id = V.VHC_ID)
SELECT *
FROM tree
By the way, what stopped the recursive process? The fact that no more chains are possible when arriving with a "NULL" value id, which is the case in this example when we reach "ALL".
Now, you get the technique. Notice that for obscure reasons, MS SQL Server 2005 does not accept the RECURSIVE key word following the WITH introducing CTE. But 2005 is a beta version actually, so we can expect that this will be solved in the final product.
5 - Hierarchical indentation
One more important thing with trees structured data is to view the data as a tree... which means a hierarchical indentation when retrieving the data. Is this possible ? Yes, of course. The order need to knows the path, the level for placing space characters and the id or the timestamp of the row in case of rows of similar tree placement (multileaves data). This can be done by calculating the path inside the recursion. Here is an example of such a query :
WITH tree (data, id, level, pathstr) AS (SELECT VHC_NAME, VHC_ID, 0, CAST('' AS VARCHAR(MAX)) FROM T_VEHICULE WHERE VHC_ID_FATHER IS NULL UNION ALL SELECT VHC_NAME, VHC_ID, t.level + 1, t.pathstr + V.VHC_NAME FROM T_VEHICULE V INNER JOIN tree t ON t.id = V.VHC_ID_FATHER) SELECT SPACE(level) + data as data, id, level, pathstr FROM tree ORDER BY pathstr, id data id level pathstr -------------------- ----------- ----------- -------------------------------- ALL 1 0 AIR 4 1 AIR PLANE 11 2 AIRPLANE ROCKET 10 2 AIRROCKET EARTH 3 1 EARTH CAR 7 2 EARTHCAR TRUCK 9 2 EARTHTRUCK TWO WHEELES 8 2 EARTHTWO WHEELES BYCYCLE 13 3 EARTHTWO WHEELESBYCYCLE MOTORCYCLE 12 3 EARTHTWO WHEELESMOTORCYCLE SEA 2 1 SEA BOAT 6 2 SEABOAT SUBMARINE 5 2 SEASUBMARINE
To do this, we have use a new data type in SQL 2005 which is called VARCHAR(MAX), because we do not know the maximum of chars that will result in an operation a concatenation of a VARCHAR(16) in a recursive query that can be very deep. Notice that it is not a good idea to construct the path with VARCHAR because it can result in some boundaries effects such as concatenating words like 'LAND' and 'MARK' as level 2 of the tree which can be confused as 'LANDMARK' as level 1 in another branch of the same tree, so you must preserve blank space in the concatened path to avoid such problems. This can be done by casting VHC_NAME as a CHAR SQL data type.
6 - Trees without recursion
But I must say that hierarchical data is not very interesting! Why? Because there are other ways to treat the data. Remember that I told you that a mathematician may say "you can avoid recursion by using a stack". Is this
possible in our case?
Yes!
Just put the stack inside the table. How? By using two new columns : RIGHT_BOUND and LEFT_BOUND...
ALTER TABLE T_VEHICULE ADD RIGHT_BOUND INTEGER ALTER TABLE T_VEHICULE ADD LEFT_BOUND INTEGER
Now, like a magician, I will populate this new columns with some tricky numbers :
UPDATE T_VEHICULE SET LEFT_BOUND = 1 , RIGHT_BOUND = 26 WHERE VHC_ID = 1 UPDATE T_VEHICULE SET LEFT_BOUND = 2 , RIGHT_BOUND = 7 WHERE VHC_ID = 2 UPDATE T_VEHICULE SET LEFT_BOUND = 8 , RIGHT_BOUND = 19 WHERE VHC_ID = 3 UPDATE T_VEHICULE SET LEFT_BOUND = 20, RIGHT_BOUND = 25 WHERE VHC_ID = 4 UPDATE T_VEHICULE SET LEFT_BOUND = 3 , RIGHT_BOUND = 4 WHERE VHC_ID = 5 UPDATE T_VEHICULE SET LEFT_BOUND = 5 , RIGHT_BOUND = 6 WHERE VHC_ID = 6 UPDATE T_VEHICULE SET LEFT_BOUND = 9 , RIGHT_BOUND = 10 WHERE VHC_ID = 7 UPDATE T_VEHICULE SET LEFT_BOUND = 11, RIGHT_BOUND = 16 WHERE VHC_ID = 8 UPDATE T_VEHICULE SET LEFT_BOUND = 17, RIGHT_BOUND = 18 WHERE VHC_ID = 9 UPDATE T_VEHICULE SET LEFT_BOUND = 21, RIGHT_BOUND = 22 WHERE VHC_ID = 10 UPDATE T_VEHICULE SET LEFT_BOUND = 23, RIGHT_BOUND = 24 WHERE VHC_ID = 11 UPDATE T_VEHICULE SET LEFT_BOUND = 12, RIGHT_BOUND = 13 WHERE VHC_ID = 12 UPDATE T_VEHICULE SET LEFT_BOUND = 14, RIGHT_BOUND = 15 WHERE VHC_ID = 13
And here is the magic query, giving the same result as the complex hierarchical recursive query :
SELECT * FROM T_VEHICULE WHERE RIGHT_BOUND > 12 AND LEFT_BOUND < 13 VHC_ID VHC_ID_FATHER VHC_NAME RIGHT_BOUND LEFT_BOUND ----------- ------------- ---------------- ----------- ----------- 1 NULL ALL 26 1 3 1 EARTH 19 8 8 3 TWO WHEELES 16 11 12 8 MOTORCYCLE 13 12
The question is : what is the trick ?
In fact we realize a stack by numbering the data slices. I make a picture of it :

The only thing I do is to numerate continuously begining by 1, from the right to the left bounds of all stacks made by each piece of data. Then to obtain the above query, I just take the bounds of the MOTORCYCLE, which are LEFT 12 and RIGHT 13, and place it in the WHERE clause asking for datas that have a RIGHT BOUND over 12 and a LEFT BOUND under 13.
By the way, my graphic will be much more clear to understand if we rotate it :
Do you see the stacks? This representation of trees is well known in specialized database litterature, especially writeings by Joe Celko. You will find every thing you want in his famous book "Trees and Hierarchies" in
"SQL for smarties", Morgan Kaufman ed. Another resource if you can read French is to go to my web site in which stored procs are written for MS SQL Server to do all jobs relative to this model : http://sqlpro.developpez.com/cours/arborescence/
Last, can we reproduce the hierarchical indentation as seen in the last query ? Yes of course. This will be much easier by introducing a new column 'LEVEL' to indicate the level of the node. This can be very simple to calculate, because when inserting in the tree, the first node is the root, so the level is 0. Another point to insert in a tree had a level that can simply be calculated with the parent's data : if the point is to insert as a son, the level is the parent level + 1. To insert as a brother, the level is the same as the brother. Here are the ALTER and UPDATE statements that place the levels in the table for our purpose :
ALTER TABLE T_VEHICULE ADD LEVEL INTEGER UPDATE T_VEHICULE SET LEVEL = 0 WHERE VHC_ID = 1 UPDATE T_VEHICULE SET LEVEL = 1 WHERE VHC_ID = 2 UPDATE T_VEHICULE SET LEVEL = 1 WHERE VHC_ID = 3 UPDATE T_VEHICULE SET LEVEL = 1 WHERE VHC_ID = 4 UPDATE T_VEHICULE SET LEVEL = 2 WHERE VHC_ID = 5 UPDATE T_VEHICULE SET LEVEL = 2 WHERE VHC_ID = 6 UPDATE T_VEHICULE SET LEVEL = 2 WHERE VHC_ID = 7 UPDATE T_VEHICULE SET LEVEL = 2 WHERE VHC_ID = 8 UPDATE T_VEHICULE SET LEVEL = 2 WHERE VHC_ID = 9 UPDATE T_VEHICULE SET LEVEL = 2 WHERE VHC_ID = 10 UPDATE T_VEHICULE SET LEVEL = 2 WHERE VHC_ID = 11 UPDATE T_VEHICULE SET LEVEL = 3 WHERE VHC_ID = 12 UPDATE T_VEHICULE SET LEVEL = 3 WHERE VHC_ID = 13
Now, the indentation query is :
SELECT SPACE(LEVEL) + VHC_NAME as data FROM T_VEHICULE ORDER BY LEFT_BOUND data ----------------------- ALL SEA SUBMARINE BOAT EARTH CAR TWO WHEELES MOTORCYCLE BYCYCLE TRUCK AIR ROCKET PLANE
Much more simple, isn't it ?
FIRST IMPRESSIONS ...
The only thing to say about these two ways of navigating through hierarchical data, is that the interval model is much more efficient and performs better than the one using
the SQL:1999 RECURSIVE query technique. In fact, RECURSIVE queries are not so interesting this way... But another way?... Yes !
7 - Second example : a complex network (a much more sexy query !)
Perhaps you never go to France. So you may be interested by the fact that in Paris, there are beautifull girls, and in Toulouse a famous dish called cassoulet, and a small plane constructor call Airbus. So the problem is to go by car from Paris to Toulouse using the speedway network. I just simplify for you (if you are lost and you do not know the prononciation to ask people your way to Toulouse, it is simple. Just say "to loose"...) :
PARIS
|
------------------------------------
| | |
385 420 470
| | |
NANTES CLERMONT FERRAND LYON
| | |
| | 335 305 | 320
| ---------- -----------------
| | | |
375 | MONTPELLIER MARSEILLE
| | |
---------------------- 205
| 240 |
TOULOUSE NICE
-- if exists, drop the table we need for the demo
IF EXISTS (SELECT *
FROM INFORMATION_SCHEMA.TABLES
WHERE TABLE_SCHEMA = USER
AND TABLE_NAME = 'T_JOURNEY')
DROP TABLE T_JOURNEY
-- create the table :
CREATE TABLE T_JOURNEY
(JNY_FROM_TOWN VARCHAR(32),
JNY_TO_TOWN VARCHAR(32),
JNY_MILES INTEGER)
-- populate :
INSERT INTO T_JOURNEY VALUES ('PARIS', 'NANTES', 385)
INSERT INTO T_JOURNEY VALUES ('PARIS', 'CLERMONT-FERRAND', 420)
INSERT INTO T_JOURNEY VALUES ('PARIS', 'LYON', 470)
INSERT INTO T_JOURNEY VALUES ('CLERMONT-FERRAND', 'MONTPELLIER', 335)
INSERT INTO T_JOURNEY VALUES ('CLERMONT-FERRAND', 'TOULOUSE', 375)
INSERT INTO T_JOURNEY VALUES ('LYON', 'MONTPELLIER', 305)
INSERT INTO T_JOURNEY VALUES ('LYON', 'MARSEILLE', 320)
INSERT INTO T_JOURNEY VALUES ('MONTPELLIER', 'TOULOUSE', 240)
INSERT INTO T_JOURNEY VALUES ('MARSEILLE', 'NICE', 205)
Now we will try a very simple query, giving all the journeys between towns :
WITH journey (TO_TOWN)
AS
(SELECT DISTINCT JNY_FROM_TOWN
FROM T_JOURNEY
UNION ALL
SELECT JNY_TO_TOWN
FROM T_JOURNEY AS arrival
INNER JOIN journey AS departure
ON departure.TO_TOWN = arrival.JNY_FROM_TOWN)
SELECT *
FROM journey
TO_TOWN
--------------------------------
CLERMONT-FERRAND
LYON
MARSEILLE
MONTPELLIER
PARIS
NANTES
CLERMONT-FERRAND
LYON
MONTPELLIER
MARSEILLE
NICE
TOULOUSE
MONTPELLIER
TOULOUSE
TOULOUSE
TOULOUSE
NICE
MONTPELLIER
MARSEILLE
NICE
TOULOUSE
MONTPELLIER
TOULOUSE
TOULOUSE
This query is not very interesting because we do not know from which town we came. We just know the towns where we can go, and the fact that we have probably different ways to go to same place. Let us see if we can have some more information...
First, we want to start from Paris :
WITH journey (TO_TOWN)
AS
(SELECT DISTINCT JNY_FROM_TOWN
FROM T_JOURNEY
WHERE JNY_FROM_TOWN = 'PARIS'
UNION ALL
SELECT JNY_TO_TOWN
FROM T_JOURNEY AS arrival
INNER JOIN journey AS departure
ON departure.TO_TOWN = arrival.JNY_FROM_TOWN)
SELECT *
FROM journey
TO_TOWN
--------------------------------
PARIS
NANTES
CLERMONT-FERRAND
LYON
MONTPELLIER
MARSEILLE
NICE
TOULOUSE
MONTPELLIER
TOULOUSE
TOULOUSE
We have probably three ways to go to Toulouse. Can we filter the destination? Sure !
WITH journey (TO_TOWN)
AS
(SELECT DISTINCT JNY_FROM_TOWN
FROM T_JOURNEY
WHERE JNY_FROM_TOWN = 'PARIS'
UNION ALL
SELECT JNY_TO_TOWN
FROM T_JOURNEY AS arrival
INNER JOIN journey AS departure
ON departure.TO_TOWN = arrival.JNY_FROM_TOWN)
SELECT *
FROM journey
WHERE TO_TOWN = 'TOULOUSE'
TO_TOWN
--------------------------------
TOULOUSE
TOULOUSE
TOULOUSE
We can refine this query by calculating the number of steps involved in the different ways :
WITH journey (TO_TOWN, STEPS)
AS
(SELECT DISTINCT JNY_FROM_TOWN, 0
FROM T_JOURNEY
WHERE JNY_FROM_TOWN = 'PARIS'
UNION ALL
SELECT JNY_TO_TOWN, departure.STEPS + 1
FROM T_JOURNEY AS arrival
INNER JOIN journey AS departure
ON departure.TO_TOWN = arrival.JNY_FROM_TOWN)
SELECT *
FROM journey
WHERE TO_TOWN = 'TOULOUSE'
TO_TOWN STEPS
-------------------------------- -----------
TOULOUSE 3
TOULOUSE 2
TOULOUSE 3
The cherry on the cake will be to know the distances of the different ways :
WITH journey (TO_TOWN, STEPS, DISTANCE) AS (SELECT DISTINCT JNY_FROM_TOWN, 0, 0 FROM T_JOURNEY WHERE JNY_FROM_TOWN = 'PARIS' UNION ALL SELECT JNY_TO_TOWN, departure.STEPS + 1, departure.DISTANCE + arrival.JNY_MILES FROM T_JOURNEY AS arrival INNER JOIN journey AS departure ON departure.TO_TOWN = arrival.JNY_FROM_TOWN) SELECT * FROM journey WHERE TO_TOWN = 'TOULOUSE' TO_TOWN STEPS DISTANCE ----------------------- ----------- ----------- TOULOUSE 3 1015 TOULOUSE 2 795 TOULOUSE 3 995
The girl in the cake will be to know the different towns we visit by those different ways :
WITH journey (TO_TOWN, STEPS, DISTANCE, WAY) AS (SELECT DISTINCT JNY_FROM_TOWN, 0, 0, CAST('PARIS' AS VARCHAR(MAX)) FROM T_JOURNEY WHERE JNY_FROM_TOWN = 'PARIS' UNION ALL SELECT JNY_TO_TOWN, departure.STEPS + 1, departure.DISTANCE + arrival.JNY_MILES, departure.WAY + ', ' + arrival.JNY_TO_TOWN FROM T_JOURNEY AS arrival INNER JOIN journey AS departure ON departure.TO_TOWN = arrival.JNY_FROM_TOWN) SELECT * FROM journey WHERE TO_TOWN = 'TOULOUSE' TO_TOWN STEPS DISTANCE WAY ----------------- ----------- ----------- ------------------------------------------------- TOULOUSE 3 1015 PARIS, LYON, MONTPELLIER, TOULOUSE TOULOUSE 2 795 PARIS, CLERMONT-FERRAND, TOULOUSE TOULOUSE 3 995 PARIS, CLERMONT-FERRAND, MONTPELLIER, TOULOUSE
And now, ladies and gentleman, the RECURSIVE QUERY is proud to present to you how to solve a very complex problem, called the traveling salesman problem. (one of the operational research problems on which Edsger Wybe Dijkstra found the first efficient algorithm and received the Turing Award in 1972):
WITH journey (TO_TOWN, STEPS, DISTANCE, WAY)
AS
(SELECT DISTINCT JNY_FROM_TOWN, 0, 0, CAST('PARIS' AS VARCHAR(MAX))
FROM T_JOURNEY
WHERE JNY_FROM_TOWN = 'PARIS'
UNION ALL
SELECT JNY_TO_TOWN, departure.STEPS + 1,
departure.DISTANCE + arrival.JNY_MILES,
departure.WAY + ', ' + arrival.JNY_TO_TOWN
FROM T_JOURNEY AS arrival
INNER JOIN journey AS departure
ON departure.TO_TOWN = arrival.JNY_FROM_TOWN)
SELECT TOP 1 *
FROM journey
WHERE TO_TOWN = 'TOULOUSE'
ORDER BY DISTANCE
TO_TOWN STEPS DISTANCE WAY
------------------ ----------- ----------- ---------------------------------
TOULOUSE 2 795 PARIS, CLERMONT-FERRAND, TOULOUSE
By the way, TOP n is a non standard SQL... Dislike it... Enjoy CTE !
WITH
journey (TO_TOWN, STEPS, DISTANCE, WAY)
AS
(SELECT DISTINCT JNY_FROM_TOWN, 0, 0, CAST('PARIS' AS VARCHAR(MAX))
FROM T_JOURNEY
WHERE JNY_FROM_TOWN = 'PARIS'
UNION ALL
SELECT JNY_TO_TOWN, departure.STEPS + 1,
departure.DISTANCE + arrival.JNY_MILES,
departure.WAY + ', ' + arrival.JNY_TO_TOWN
FROM T_JOURNEY AS arrival
INNER JOIN journey AS departure
ON departure.TO_TOWN = arrival.JNY_FROM_TOWN),
short (DISTANCE)
AS
(SELECT MIN(DISTANCE)
FROM journey
WHERE TO_TOWN = 'TOULOUSE')
SELECT *
FROM journey j
INNER JOIN short s
ON j.DISTANCE = s.DISTANCE
WHERE TO_TOWN = 'TOULOUSE'
8 - What more can we do?
In fact, one thing that is limiting the process in our network of speedways, is that we have made routes with a single sense. I mean, we can go from Paris to Lyon, but we are not allowed to go from Lyon to
Paris. For that, we need to add the reverse ways in the table, like :
JNY_FROM_TOWN JNY_TO_TOWN JNY_MILES -------------- ------------ --------- LYON PARIS 470
This can be done, by a very simple query :
INSERT INTO T_JOURNEY SELECT JNY_TO_TOWN, JNY_FROM_TOWN, JNY_MILES FROM T_JOURNEY
The only problem is that, previous queries won't work properly :
WITH journey (TO_TOWN)
AS
(SELECT DISTINCT JNY_FROM_TOWN
FROM T_JOURNEY
WHERE JNY_FROM_TOWN = 'PARIS'
UNION ALL
SELECT JNY_TO_TOWN
FROM T_JOURNEY AS arrival
INNER JOIN journey AS departure
ON departure.TO_TOWN = arrival.JNY_FROM_TOWN)
SELECT *
FROM journey
TO_TOWN
--------------------------------
PARIS
NANTES
CLERMONT-FERRAND
LYON
...
LYON
MONTPELLIER
MARSEILLE
PARIS
Msg 530, Level 16, State 1, Line 1
The statement terminated. The maximum recursion 100 has been exhausted before statement completion.
What happened? Simply, you are trying all ways including cycling ways like Paris, Lyon, Paris, Lyon, Paris... ad infinitum... Is there a way to avoid cycling routes? Maybe. In one of our previous queries, we have a column that give the complete list of stepped towns. Why don't we use it to avoid cycleing? The condition will be : do not pass through a town that is already in the WAY. This can be written as :
WITH journey (TO_TOWN, STEPS, DISTANCE, WAY)
AS
(SELECT DISTINCT JNY_FROM_TOWN, 0, 0, CAST('PARIS' AS VARCHAR(MAX))
FROM T_JOURNEY
WHERE JNY_FROM_TOWN = 'PARIS'
UNION ALL
SELECT JNY_TO_TOWN, departure.STEPS + 1,
departure.DISTANCE + arrival.JNY_MILES,
departure.WAY + ', ' + arrival.JNY_TO_TOWN
FROM T_JOURNEY AS arrival
INNER JOIN journey AS departure
ON departure.TO_TOWN = arrival.JNY_FROM_TOWN
WHERE departure.WAY NOT LIKE '%' + arrival.JNY_TO_TOWN + '%')
SELECT *
FROM journey
WHERE TO_TOWN = 'TOULOUSE'
TO_TOWN STEPS DISTANCE WAY
-------------- ----------- ----------- ---------------------------------------------------------
TOULOUSE 3 1015 PARIS, LYON, MONTPELLIER, TOULOUSE
TOULOUSE 4 1485 PARIS, LYON, MONTPELLIER, CLERMONT-FERRAND, TOULOUSE
TOULOUSE 2 795 PARIS, CLERMONT-FERRAND, TOULOUSE
TOULOUSE 3 995 PARIS, CLERMONT-FERRAND, MONTPELLIER, TOULOUSE
As you see, a new route occurs. The worst in distance, but perhaps the most beautifull !
CONCLUSIONS
A CTE can simplify the expression of complex queries. RECURSIVE queries must be employed where recursivity is needed. If you make a bad query with MS SQL Server, don't be afraid, the cycles of recursions are limited to
100. You can overcome this limit by fixing OPTION (MAXRECURSION n), with n as the value you want. The OPTION clause must be the last one in a CTE expression. But remember one thing : MS SQL Server 2005 is actually
a beta version!
Last but not least, ISO SQL:1999 had some more syntax options that can allow you to navigate in the data DEPTH FIRST or BREADTH FIRST, and also to all the data contained in the steps (in an ARRAY of ROW which must be of "sufficient" in dimension to cover all cases !).
Here is the syntax :
WITH [ RECURSIVE ][ ( <liste_colonne> ) ] AS ( <requete_select> ) [ <clause_cycle_recherche> ] with : <clause_cycle_recherche> ::= <clause_recherche> | <clause_cycle> | <clause_recherche> <clause_cycle> and : <clause_recherche> ::= SEARCH { DEPTH FIRTS BY | BREADTH FIRST BY } <liste_specification_ordre> SET <colonne_sequence> <clause_cycle> ::= CYCLE <colonne_cycle1> [ { , <colonne_cycle2> } ... ] SET <colonne_marquage_cycle> TO <valeur_marque_cycle> DEFAULT <valeur_marque_non_cycle> USING <colonne_chemin>
Bonus (CTE, recursive query applied)
Here is a query in a SP, that can give the exact order of tables do delete before deleting a target table, due to referential integrity :
CREATE PROCEDURE P_WHAT_TO_DELETE_BEFORE
@TABLE_TO_DELETE VARCHAR(128), -- targettable to delete
@DB VARCHAR(128), -- target database
@USR VARCHAR(128) -- target schema (dbo in most cases)
AS
WITH T_CONTRAINTES (table_name, father_table_name)
AS (SELECT DISTINCT CTU.TABLE_NAME, TCT.TABLE_NAME
FROM INFORMATION_SCHEMA.REFERENTIAL_CONSTRAINTS RFC
INNER JOIN INFORMATION_SCHEMA.CONSTRAINT_TABLE_USAGE CTU
ON RFC.CONSTRAINT_CATALOG = CTU.CONSTRAINT_CATALOG
AND RFC.CONSTRAINT_SCHEMA = CTU.CONSTRAINT_SCHEMA
AND RFC.CONSTRAINT_NAME = CTU.CONSTRAINT_NAME
INNER JOIN INFORMATION_SCHEMA.TABLE_CONSTRAINTS TCT
ON RFC.UNIQUE_CONSTRAINT_CATALOG = TCT.CONSTRAINT_CATALOG
AND RFC.UNIQUE_CONSTRAINT_SCHEMA = TCT.CONSTRAINT_SCHEMA
AND RFC.UNIQUE_CONSTRAINT_NAME = TCT.CONSTRAINT_NAME
WHERE CTU.TABLE_CATALOG = @DB
AND CTU.TABLE_SCHEMA = @USR)
,T_TREE_CONTRAINTES (table_to_delete, level)
AS (SELECT DISTINCT table_name, 0
FROM T_CONTRAINTES
WHERE father_table_name = @TABLE_TO_DELETE
UNION ALL
SELECT priorT.table_name, level - 1
FROM T_CONTRAINTES priorT
INNER JOIN T_TREE_CONTRAINTES beginT
ON beginT.table_to_delete = priorT.father_table_name
WHERE priorT.father_table_name priorT.table_name)
SELECT DISTINCT *
FROM T_TREE_CONTRAINTES
ORDER BY level
GO
The self-reference case has been integrated. The parameters are :
@DB (database name),
@USR (schema name : dbo),
@TABLE_TO_DELETE (table you want to delete).
Bibliographical list :
- Le langage SQL : Frédéric Brouard, Christian Soutou
- Pearson Education 2005 (France)
- Joe Celko's Trees & Hierarchies in SQL for Smarties : Joe
Celko - Morgan Kaufmann 2004
- SQL:1999 : J. Melton, A. Simon - Morgan Kauffman, 2002
- SQL développement : Frédéric Brouard -
Campus Press 2001 (France)
- SQL for Dummies : Allen G. Taylor - Hungry Minds Inc 2001
- SQL-99 complete really : P. Gulutzan, T. Pelzer - R&D Books,
1999
- SQL 3, Implementing the SQL Foundation Standard : Paul Fortier -
Mc Graw Hill, 1999
- SQL for smarties : Joe Celko - Morgan Kaufmann 1995
On Dijkstra shortest path algorithm for the traveling salesman problem and other operational research problem, see :
http://www.hsor.org/downloads/Speedy_Delivery_teacher.pdf
About cassoulet :
Discussion : http://www.evevancouver.ca/food/dishes/cassoulet.htm
Impressions : http://www.taunton.com/finecooking/pages/c00081.asp
The Academy of the Cassoulet : http://www.routedescassoulets.com/auc_uk/auc_presentation_uk.htm



